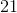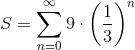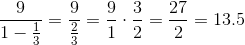Sums of Infinite Series
Help Questions
Pre-Calculus › Sums of Infinite Series
What is the sum of the alternating series below?
Explanation
The alternating series follows a geometric pattern.
We can evaluate the geometric series from the formula.
What is the sum of the following infinite series?
diverges
Explanation
This series is not alternating - it is the mixture of two geometric series.
The first series has the positive terms.
The second series has the negative terms.
The sum of these values is 3.5.
Find the sum of the following infinite series:
Explanation
Notice that this is an infinite geometric series, with ratio of terms = 1/3. Hence it can be rewritten as:
Since the ratio, 1/3, has absolute value less than 1, we can find the sum using this formula:
Where 

In the infinite series 



170
-64
128
210
-256
Explanation
Once you're identified the pattern in the series, you might see a quick way to perform the summation. Since the base of the exponent for each term is negative, the result will be positive if 
-2, 4, -8, 16, -32, 64, -128, 256
Note that each "pair" of adjacent numbers has one negative and one positive. for the first pair, -2 + 4 = 2. For the second, -8 + 16 = 8. For the third, -32 + 64 = 32. And so for the fourth, -128 + 256 = 128. You can then quickly sum the values to see that the answer is 170.
Evaluate:
The series does not converge.
Explanation
This is a geometric series whose first term is 

Evaluate:
The series does not converge.
Explanation
This is a geometric series whose first term is 

Find the value for
Explanation
To best understand, let's write out the series. So
We can see this is an infinite geometric series with each successive term being multiplied by 
A definition you may wish to remember is