Gases

Help Questions

Physical Chemistry › Gases

Questions 1 - 10

A sample of argon gas at a pressure of 0.959atm and a temperature of , occupies a volume of 563mL. If the gas is compressed at constant temperature until its pressure is 1.40atm, what will be the final volume of the sample of gas?

Explanation

The argon gas, as the problem states, is under constant temperature with varying volume and pressure, so we need to use Boyle's Law:

$P_{1}V{_{1}}=P_{2}V{_{2}}$

We are given the initial pressure, the initial volume, and the final pressure, and need to solve for the final volume. Therefore, we can rearrange Boyle's law to be as follows:

$\frac{(P{_{1}}V_{1})}{P{_{2}}} = V_{2}$

Plug in known values and solve.

$V_2=\frac{0.959*563}{1.4}$

$V_2 \approx 386mL$

An unknown gas is being analyzed in lab. You place of this gas in a container at $27^\circ C$ . You observe that the pressure and volume of the gas is and , respectively. What is the identity of the gas? Assume the gas behaves ideally.

Oxygen

Nitrogen

Argon

Chlorine

Explanation

To solve this question we need to use the ideal gas law equation:

Above, is pressure in , is volume in liters, is moles, is $0.08206 \frac{L\cdot atm}{mol\cdot K}$ , and is temperature in Kelvins. The question gives us pressure, volume, and temperature; therefore, we can solve for . First, we need to convert temperature from Celsius to Kelvins.

$Kelvin = ^\circ C + 273.15$

$T = 27^\circ C+ 273.15 = 300.15K$

Rearrange the ideal gas law and solve for :

$n = \frac{PV}{RT}$
$n = \frac{(1.54atm)(0.5L)}{(300.15K)(0.08206\frac{L\cdot atm}{mol\cdot K})}$

The question states that you place one gram of gas in the container. Since we know the moles, we can solve for the molecular weight of the gas and figure out its identity from the molecular weight.

$MW = \frac{1g}{0.0312mol} = \frac{32g}{mol}$

The molecular weight of oxygen gas, is $32\frac{g}{mol}$ ; therefore, the unknown gas must be oxygen.

At constant temperature and moles, which of the following is true regarding pressure and volume of a gas?

Pressure and volume have a linear relationship with a positive correlation

Pressure and volume are independent of each other

Pressure and volume have an exponential relationship with a negative correlation

Pressure and volume have an exponential relationship with a positive correlation

Explanation

First, we need to figure out which gas law is applicable here. The question states that temperature and moles are constant. This means that we are dealing with Boyle’s law, which states that pressure is inversely proportional to volume. Inversely proportional means that the pressure decreases as volume increases and vice versa. Note that the relationship is still linear (change in one variable causes a proportional change in the other variable), but the two variables have a negative correlation. Positive correlation means increasing or decreasing a variable would also increase or decrease the other variable, respectively.

Explanation

The argon gas, as the problem states, is under constant temperature with varying volume and pressure, so we need to use Boyle's Law:

$P_{1}V{_{1}}=P_{2}V{_{2}}$

We are given the initial pressure, the initial volume, and the final pressure, and need to solve for the final volume. Therefore, we can rearrange Boyle's law to be as follows:

$\frac{(P{_{1}}V_{1})}{P{_{2}}} = V_{2}$

Plug in known values and solve.

$V_2=\frac{0.959*563}{1.4}$

$V_2 \approx 386mL$

Oxygen

Nitrogen

Argon

Chlorine

Explanation

To solve this question we need to use the ideal gas law equation:

$Kelvin = ^\circ C + 273.15$

$T = 27^\circ C+ 273.15 = 300.15K$

Rearrange the ideal gas law and solve for :

$n = \frac{PV}{RT}$
$n = \frac{(1.54atm)(0.5L)}{(300.15K)(0.08206\frac{L\cdot atm}{mol\cdot K})}$

The question states that you place one gram of gas in the container. Since we know the moles, we can solve for the molecular weight of the gas and figure out its identity from the molecular weight.

$MW = \frac{1g}{0.0312mol} = \frac{32g}{mol}$

The molecular weight of oxygen gas, is $32\frac{g}{mol}$ ; therefore, the unknown gas must be oxygen.

At constant temperature and moles, which of the following is true regarding pressure and volume of a gas?

Pressure and volume have a linear relationship with a positive correlation

Pressure and volume are independent of each other

Pressure and volume have an exponential relationship with a negative correlation

Pressure and volume have an exponential relationship with a positive correlation

Explanation

Given the ideal gas law:

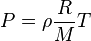
$\ P = \rho \frac{R}{M}T$

Where $\small \rho$ is density, is pressure, is the gas constant, is molar mass, and is temperature.

Based on the Ideal gas law, which of the following are true?

I. Pressure and volume are inversely proportional

II. Pressure and density are inversely proportional

III. Pressure and temperature are directly proportional

IV. Density and temperature are inversely proportional

V. R and M are inversely proportional

I, III, IV

I, II, III, IV, V

I, III

II, III, V

III, IV, V

Explanation

Condition I is true. Pressure and volume are inversely proportional. The ideal gas law with volume can be rederived to show this:

We introduce an expression for moles:

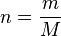
$n = {\frac{m}{M}}$ $\small (1)$

Where is moles, is mass, and is molar mass in $\frac{g}{mol}$

Rearranging (1) to solve for and plugging into the following:

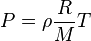
$\ P = \rho \frac{R}{M}T$

We get:

$P = \rho \frac{Rn}{m}T$ (2)

Finally, we use the following for density, where is volume, and plug into (2)

$\rho = \frac{m}{V}$

$P = \frac{m}{V}\cdot \frac{Rn}{m}T$

The masses cancel out and we have the ideal gas law expressed with volume and moles.

Condition II is false. It is clear from the equation that pressure and density are directly proportional.

Condition III is true because it is clear from the equation that temperature and pressure are directly proportional.

Condition IV is true because density and temperature are on the same side of the equation in the numerator, so the must be inversely proportional.

Condition V is false because the ideal gas constant and molar mass can be rearranged to be on opposite sides of the equation and in the numerator.

A researcher places a closed piston container at room temperature. He places a Bunsen burner at the bottom of the container and observes that the piston moves up. What can best explain this phenomenon?

The volume of the gas increased because of Charles’ Law

The pressure of the gas decreased because of Charles’ Law

The volume of the gas increased because of Boyle’s Law

The pressure of the gas decreased because of Boyle’s Law

Explanation

There are three main gas laws. Avogadro’s law states that the moles of a gas is directly proportional to the volume (under constant pressure and temperature). Boyle’s law states that the pressure of the gas is inversely proportional to the volume (under constant moles and temperature). This means that the pressure decreases proportionally when the volume increases. Charles’ law states that the temperature is directly proportional to the volume (under constant moles and pressure). The question states that the piston moves up. This means that the volume of the gas is expanding inside and pushing the piston up to make room for the expanding gas. The gas expansion occurs due to increased temperature (Charles’ law).

The volume of the gas increased because of Charles’ Law

The pressure of the gas decreased because of Charles’ Law

The volume of the gas increased because of Boyle’s Law

The pressure of the gas decreased because of Boyle’s Law

Explanation

Given the van der Waals Equation:

$P = \frac{nRT}{V-nb}-\frac{n^2a}{V^2}$

Which statement accurately identifies and explains the corrections that van der Waals made to the ideal gas law, where the first correction is the $\small -nb$ term and the second correction is the $-\frac{n^2a}{V^2}$ term?

The first correction corrects for volume of molecules by decreasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by decreasing pressure as volume decreases and number of molecules increases.

The first correction corrects for volume of molecules by increasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by decreasing pressure as volume increases and number of molecules increases.

The first correction corrects for volume of molecules by increasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by increasing pressure as volume increases and number of molecules increases.

The first correction corrects for volume of molecules by decreasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by increasing pressure as volume increases and number of molecules increases.

The first correction corrects for volume of molecules by increasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by increasing pressure as volume decreases and number of molecules increases.

Explanation

All the statements say similar things, but only one correctly identifies the resulting change to volume and pressure. Let's break things down by the correction.

Correction 1:

The correction decreases the volume, since it is subtracting $\small \small nb$ from the overall volume. As n (or the number of molecules) goes up, volume will go down.

Correction 2:

Since we are subtracting $\frac{n^2a}{V^2}$ from the overall pressure, we are correcting for molecular attraction by decreasing pressure. We are doing this with a term $\frac{n^2a}{V^2}$ that gets largerwhen increases and and gets larger as decreases.

Page 1 of 2

Return to subject

AI TutorYour personal study buddy

Question of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

WorksheetsBuild custom practice quizzes

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Diagnostic TestsAssess your knowledge level

Practice TestsTest your skills with exam questions

GamesLearn through free games