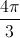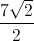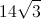All High School Math Resources
Example Questions
Example Question #56 : The Unit Circle And Radians
How many radians are in 
To convert degrees to radians, set up a ratio. The ratio of degrees to radians is 
Cross multiply.
Example Question #57 : The Unit Circle And Radians
How many radians are in 
To solve this, use a proportion. The ratio of degrees to radians is 
Cross multiply:
Example Question #81 : Trigonometry
In the unit circle, what is the angle in radians that corresponds to the point (0, -1)?
On the unit circle, (0,-1) is the point that falls between the third and fourth quadrant. This corresponds to 
Example Question #82 : Trigonometry
What is the reference angle for 
To find the reference angle, subtract 
Example Question #1 : Triangles
 In this figure, side
In this figure, side 



Undefined
Since 
That means that 
In this problem, that would be:
Plug in our given values:
Example Question #1 : Applying Trigonometric Functions
Let ABC be a right triangle with sides 






We are looking for 

So therefore, without figuring out 
Example Question #83 : Trigonometry

In this figure, if angle 



Undefined
Since 
That means that 
In this problem, that would be:
Plug in our given values:
Example Question #84 : Trigonometry

In this figure, 



Undefined
Notice that these sides fit the pattern of a 30:60:90 right triangle: 
In this case, 
Since angle 


Example Question #85 : Trigonometry
A triangle has angles of 



The pattern for 

If the side opposite 



Example Question #2 : Triangles
In 




A triangle with these sidelengths cannot exist.
By the Triangle Inequality, this triangle can exist, since 
By the Law of Cosines:
Substitute the sidelengths and solve for 
All High School Math Resources