All High School Math Resources
Example Questions
Example Question #1 : How To Find The Area Of A Sector
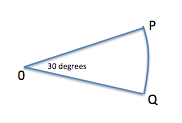
In the figure, PQ is the arc of a circle with center O. If the area of the sector is 
Possible Answers:
Correct answer:
Explanation:
First, we figure out what fraction of the circle is contained in sector OPQ: 

Using the formula for the area of a circle, 

We can use this to solve for the circumference of the circle, 

Now, OP and OQ are both equal to r, and PQ is equal to 
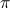
To get the perimeter, we add OP + OQ + PQ, which give us 
All High School Math Resources
Popular Subjects
Biology Tutors in Los Angeles, Physics Tutors in San Francisco-Bay Area, GMAT Tutors in Houston, French Tutors in Philadelphia, Algebra Tutors in San Francisco-Bay Area, SSAT Tutors in Dallas Fort Worth, LSAT Tutors in Boston, Chemistry Tutors in Los Angeles, MCAT Tutors in Miami, Spanish Tutors in Atlanta
Popular Courses & Classes
ISEE Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Chicago, GMAT Courses & Classes in Miami, ISEE Courses & Classes in San Diego, MCAT Courses & Classes in Miami, ISEE Courses & Classes in Chicago, SAT Courses & Classes in Miami, GMAT Courses & Classes in Philadelphia, SAT Courses & Classes in Denver, GMAT Courses & Classes in Phoenix
Popular Test Prep
MCAT Test Prep in Miami, GMAT Test Prep in Los Angeles, SAT Test Prep in Philadelphia, MCAT Test Prep in Philadelphia, GMAT Test Prep in San Diego, MCAT Test Prep in Seattle, ISEE Test Prep in San Diego, SAT Test Prep in Los Angeles, GRE Test Prep in Miami, GMAT Test Prep in Philadelphia