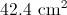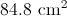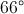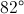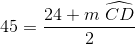Math - Circles | Practice Hub

Find the area of the following sector:

$9 \pi\ m^2$

$18 \pi\ m^2$

$6 \pi\ m^2$

$3 \pi\ m^2$

$12 \pi\ m^2$

Explanation

The formula for the area of a sector is

$A = \pi r^2 (part)$ ,

where is the radius of the circle and is the fraction of the sector.

Plugging in our values, we get:

$A = \pi (6\ m)^2 (\frac{90}{360})$

$A=9 \pi\ m^2$

To the nearest tenth, give the area of a $60^{\circ }$ sector of a circle with diameter 18 centimeters.

$42.4 \textrm{ cm}^{2}$

$84.8 \textrm{ cm}^{2}$

$169.6 \textrm{ cm}^{2}$

$21.2 \textrm{ cm}^{2}$

$254.5 \textrm{ cm}^{2}$

Explanation

The radius of a circle with diameter 18 centimeters is half that, or 9 centimeters. The area of a $60^{\circ }$ sector of the circle is

$A = \frac{60}{360 }\cdot \pi \cdot 9^{2} =\frac{1}{6} \cdot \pi \cdot 81 \approx 42.4 \textrm{ cm}^{2}$

Find the area of the shaded region:

Screen_shot_2014-02-27_at_6.35.30_pm

$108\pi-81\sqrt{3}m^2$

$108\pi-81\sqrt{2}m^2$

$81\pi-81\sqrt{3}m^2$

$108\pi-108\sqrt{3}m^2$

$81\pi-108\sqrt{3}m^2$

Explanation

To find the area of the shaded region, you must subtract the area of the triangle from the area of the sector.

The formula for the shaded area is:

$A=A_{sector}-A_{triangle}$

$A = \pi(r^2)(part)-\frac{1}{2}(b)(h)$ ,

where is the radius of the circle, is the fraction of the sector, is the base of the triangle, and is the height of the triangle.

In order to the find the base and height of the triangle, use the formula for a triangle:

$a-a\sqrt{3}-2a$ , where is the side opposite the $\measuredangle30$ .

Plugging in our final values, we get:

$A = \pi(18m^2)(\frac{120}{360})-\frac{1}{2}(18\sqrt{3}m)(9m)$

$A = 108\pi-81\sqrt{3}m^2$

Find the area of the following sector:

$9 \pi\ m^2$

$18 \pi\ m^2$

$6 \pi\ m^2$

$3 \pi\ m^2$

$12 \pi\ m^2$

Explanation

The formula for the area of a sector is

$A = \pi r^2 (part)$ ,

where is the radius of the circle and is the fraction of the sector.

Plugging in our values, we get:

$A = \pi (6\ m)^2 (\frac{90}{360})$

$A=9 \pi\ m^2$

Find the area of the shaded region:

Screen_shot_2014-02-27_at_6.35.30_pm

$108\pi-81\sqrt{3}m^2$

$108\pi-81\sqrt{2}m^2$

$81\pi-81\sqrt{3}m^2$

$108\pi-108\sqrt{3}m^2$

$81\pi-108\sqrt{3}m^2$

Explanation

To find the area of the shaded region, you must subtract the area of the triangle from the area of the sector.

The formula for the shaded area is:

$A=A_{sector}-A_{triangle}$

$A = \pi(r^2)(part)-\frac{1}{2}(b)(h)$ ,

where is the radius of the circle, is the fraction of the sector, is the base of the triangle, and is the height of the triangle.

In order to the find the base and height of the triangle, use the formula for a triangle:

$a-a\sqrt{3}-2a$ , where is the side opposite the $\measuredangle30$ .

Plugging in our final values, we get:

$A = \pi(18m^2)(\frac{120}{360})-\frac{1}{2}(18\sqrt{3}m)(9m)$

$A = 108\pi-81\sqrt{3}m^2$

Arcs

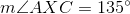
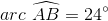
$m \angle AXC = 135^{\circ }$ ; $arc\ \widehat{AB} = 24^{\circ }$ ; $arc\ \widehat{AC} = 94^{\circ }$

Find the degree measure of $arc\ \widehat{CD}$ .

$66^{\circ }$

Not enough information is given to answer this question.

$164^{\circ}$

$82^{\circ}$

$132^{\circ }$

Explanation

When two chords of a circle intersect, the measure of the angle they form is half the sum of the measures of the arcs they intercept. Therefore,

$m \angle AXB = \frac{m; \widehat{AB} + m; \widehat{CD} }{2}$

Since $\angle AXB$ and $\angle AXC$ form a linear pair, $m \angle AXB + m \angle AXC = 180$ , and $m \angle AXB = 180 - m \angle AXC = 180 - 135 = 45^{\circ }$ .

Substitute $m; \widehat{AB} = 24$ and $m \angle AXB = 45$ into the first equation:

$45 = \frac{24 + m; \widehat{CD} }{2}$

$90 =24 + m; \widehat{CD}$

$66 = m; \widehat{CD}$

Circle_graph_area3

100_π_

50_π_

25_π_

10_π_

20_π_

Explanation

Circle_graph_area2

To the nearest tenth, give the area of a $60^{\circ }$ sector of a circle with diameter 18 centimeters.

$42.4 \textrm{ cm}^{2}$

$84.8 \textrm{ cm}^{2}$

$169.6 \textrm{ cm}^{2}$

$21.2 \textrm{ cm}^{2}$

$254.5 \textrm{ cm}^{2}$

Explanation

The radius of a circle with diameter 18 centimeters is half that, or 9 centimeters. The area of a $60^{\circ }$ sector of the circle is

$A = \frac{60}{360 }\cdot \pi \cdot 9^{2} =\frac{1}{6} \cdot \pi \cdot 81 \approx 42.4 \textrm{ cm}^{2}$

Arcs

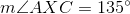
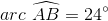
$m \angle AXC = 135^{\circ }$ ; $arc\ \widehat{AB} = 24^{\circ }$ ; $arc\ \widehat{AC} = 94^{\circ }$

Find the degree measure of $arc\ \widehat{CD}$ .

$66^{\circ }$

Not enough information is given to answer this question.

$164^{\circ}$

$82^{\circ}$

$132^{\circ }$

Explanation

When two chords of a circle intersect, the measure of the angle they form is half the sum of the measures of the arcs they intercept. Therefore,

$m \angle AXB = \frac{m; \widehat{AB} + m; \widehat{CD} }{2}$

Since $\angle AXB$ and $\angle AXC$ form a linear pair, $m \angle AXB + m \angle AXC = 180$ , and $m \angle AXB = 180 - m \angle AXC = 180 - 135 = 45^{\circ }$ .

Substitute $m; \widehat{AB} = 24$ and $m \angle AXB = 45$ into the first equation:

$45 = \frac{24 + m; \widehat{CD} }{2}$

$90 =24 + m; \widehat{CD}$

$66 = m; \widehat{CD}$

A square with a side length of 4 inches is inscribed in a circle, as shown below. What is the area of the unshaded region inside of the circle, in square inches?

Act_math_01

8π - 16

4π-4

8π-4

2π-4

8π-8

Explanation

Using the Pythagorean Theorem, the diameter of the circle (also the diagonal of the square) can be found to be 4√2. Thus, the radius of the circle is half of the diameter, or 2√2. The area of the circle is then π(2√2)2, which equals 8π. Next, the area of the square must be subtracted from the entire circle, yielding an area of 8π-16 square inches.

Circles

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation