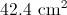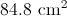Geometry
Help Questions
Math › Geometry
Find the area of the following sector:

Explanation
The formula for the area of a sector is

where 

Plugging in our values, we get:
Which is the greater quantity?
(a) The sidelength of a square with area 
(b) The sidelength of a square with perimeter 
(a) is greater.
(b) is greater.
(a) and (b) are equal.
It is impossible to tell which is greater from the information given.
Explanation
The sidelength of a square is the square root of its area and one-fourth of its perimeter, so:
(a) A square with area 

(b) A square with perimeter 

(a) is the greater quantity.
To the nearest tenth, give the area of a circle with diameter 17 inches.
Explanation
The radius of a circle with diameter 17 inches is half that, or 8.5 inches. The area of the circle is
To the nearest tenth, give the area of a 
Explanation
The radius of a circle with diameter 18 centimeters is half that, or 9 centimeters. The area of a 
What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?
100
100√2
50√2
50
200√2
Explanation

(A) The volume of a cube with edges of length
(B) The volume of a sphere with radius
(A) is greater
(B) is greater
(A) and (B) are equal
It is impossible to determine which is greater from the information given
Explanation
No calculation is really needed here, as a sphere with radius 


A pentagon with a perimeter of one mile has three congruent sides. The second-longest side is 250 feet longer than any one of those three congruent sides, and the longest side is 500 feet longer than the second-longest side.
Which is the greater quantity?
(a) The length of the longest side of the pentagon
(b) Twice the length of one of the three shortest sides of the pentagon
(b) is greater.
(a) is greater.
(a) and (b) are equal.
It is impossible to tell from the information given.
Explanation
If each of the five congruent sides has measure 





Now we can compare (a) and (b).
(a) The longest side has measure 
(b) The three shortest sides each have length 856 feet; twice this is 
(b) is greater.
A rectangular postage stamp has a width of 3 cm and a height of 12 cm. Find the area of the stamp.
Explanation
A rectangular postage stamp has a width of 3 cm and a height of 12 cm. Find the area of the stamp.
To find the area of a rectangle, we must perform the following:
Where l and w are our length and width.
This means we need to multiply the given measurements. Be sure to use the right units!
And we have our answer. It must be centimeters squared, because we are dealing with area.

The above rectangle, which has perimeter 360, is divided into squares of equal size. Give the area of the shaded portion.
Explanation
The sides of the rectangle, in total, are divided into 18 segments of equal measure, as indicated below:

The rectangle has a total perimeter of 360, so each segment - one side of a square - measures 


Determine the area of a circle with a diameter of 
Explanation
Write the formula for the area of a circle.
The radius is half the diameter, 
Substitute the radius into the equation.
The answer is: