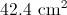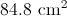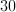Geometry
Help Questions
Math › Geometry
A right triangle has legs of 15m and 20m. What is the length of the hypotenuse?
30m
45m
35m
40m
25m
Explanation
The Pythagorean theorem is a2 + b2 = c2, where a and b are legs of the right triangle, and c is the hypotenuse.
(15)2 + (20)2 = c2 so c2 = 625. Take the square root to get c = 25m
An isoceles triangle has a base angle that is twice the vertex angle. What is the sum of the base and vertex angles?
Explanation
All triangles have 
Let 

So the equation to solve becomes:

Thus 

The sum of the vertex and one base angle is 
To the nearest tenth, give the area of a 
Explanation
The radius of a circle with diameter 18 centimeters is half that, or 9 centimeters. The area of a 
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Explanation
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 
Find the area of the following kite:

Explanation
The formula for the area of a kite is:
Where 

Plugging in our values, we get:
The perimeter of a square is 48. What is the length of its diagonal?
Explanation
Perimeter = side * 4
48 = side * 4
Side = 12
We can break up the square into two equal right triangles. The diagonal of the sqaure is then the hypotenuse of these two triangles.
Therefore, we can use the Pythagorean Theorem to solve for the diagonal:
A cube has a side length of 
Explanation
The formula for the volume of a cube is:
Since the length of one side is 

Find the area of the shaded region:

Explanation
To find the area of the shaded region, you must subtract the area of the triangle from the area of the sector.
The formula for the shaded area is:

where 



In order to the find the base and height of the triangle, use the formula for a 



Plugging in our final values, we get:
What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?
100
100√2
50√2
50
200√2
Explanation
To the nearest tenth, give the area of a 
Explanation
The radius of a circle with diameter 18 centimeters is half that, or 9 centimeters. The area of a