All High School Math Resources
Example Questions
Example Question #1 : How To Find The Surface Area Of A Polyhedron
Find the surface area of the following polyhedron.

The formula for the surface area of the polyhedron is:
Where 


Use the formula for a 
Plugging in our values, we get:
Example Question #3 : Other Polyhedrons
Find the surface area of the following polyhedron.

The formula for the surface area of the polyhedron is:
where 



Use the formula for a 
Plugging in our values, we get:
Example Question #2 : How To Find The Surface Area Of A Polyhedron
Find the surface area of the following polyhedron.

The formula for the surface area of a polyhedron is:
where 

Use the formula for a 
Plugging in our values, we get:
Example Question #1 : Other Polyhedrons
Find the volume of the following half cylinder.
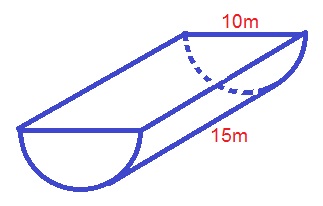
The formula for the volume of a half-cylinder is:
where 

Plugging in our values, we get:
Example Question #6 : Other Polyhedrons
Find the volume of the following polyhedron.

The formula for the volume of the polyhedron is:
Where 


Use the formula for a 
Plugging in our values, we get:
Example Question #1 : Other Polyhedrons
Find the volume of the following polyhedron.

The formula for the volume of the polyhedron is:
where 



Use the formula for a 
Plugging in our values, we get:
Example Question #8 : Other Polyhedrons
Find the volume of the following polyhedron.

The formula for the volume of the polyhedron is:
where 

Use the formula for a 
Plugging in our values, we get:
Example Question #1 : Cubes
Our backyard pool holds 10,000 gallons. Its average depth is 4 feet deep and it is 10 feet long. If there are 7.48 gallons in a cubic foot, how wide is the pool?
33 ft
7.48 ft
133 ft
100 ft
30 ft
33 ft
There are 7.48 gallons in cubic foot. Set up a ratio:
1 ft3 / 7.48 gallons = x cubic feet / 10,000 gallons
Pool Volume = 10,000 gallons = 10,000 gallons * (1 ft3/ 7.48 gallons) = 1336.9 ft3
Pool Volume = 4ft x 10 ft x WIDTH = 1336.9 cubic feet
Solve for WIDTH:
4 ft x 10 ft x WIDTH = 1336.9 cubic feet
WIDTH = 1336.9 / (4 x 10) = 33.4 ft
Example Question #921 : Act Math
A cube has a volume of 64cm3. What is the area of one side of the cube?
16cm3
4cm2
16cm
4cm
16cm2
16cm2
The cube has a volume of 64cm3, making the length of one edge 4cm (4 * 4 * 4 = 64).
So the area of one side is 4 * 4 = 16cm2
Example Question #2 : How To Find The Length Of An Edge Of A Cube
Given that the suface area of a cube is 72, find the length of one of its sides.
The standard equation for surface area is
where 

Certified Tutor
Certified Tutor
All High School Math Resources