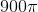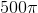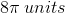Solid Geometry

Help Questions

Math › Solid Geometry

Questions 1 - 10

If the diameter of a sphere is , what is the surface area?

$225\pi$

$900\pi$

$42\pi$

$500\pi$

$56.25\pi$

Explanation

The radius is half the length of a diameter.

$r=\frac{d}{2}=\frac{15}{2}=7.5$

Write the formula for the surface area of a sphere and plug in the radius.

$A=4\pi r^2 = 4\pi(7.5)^2= 225\pi$

The diameter of a sphere is . What is the sphere's surface area?

Explanation

The equation to find the surface area of a sphere is: $Area = 4 \cdot \pi \cdot r^2$

The only information required to solve for the area is the radius. This information is given to us in a sense. If the diameter of the sphere is , the radius must be . This is because the radius is equivalent to half of the diameter.

Now that we know the radius, we can solve for the area by substituting in for the value of , the radius.

$Area = 4 \cdot \pi \cdot (4^2)$

$A = 4 \cdot \pi \cdot 16$

$A = 64 \cdot \pi$

If the radius of the sphere is one half, what is the surface area?

$\pi$

$\frac{1}{4}\pi$

$\frac{1}{2}\pi$

$\frac{4}{3}\pi$

$2\pi$

Explanation

Write the formula for the surface area of a sphere, plug in the radius, and find the area.

$A=4\pi r^2 = 4\pi \left(\frac{1}{2}\right)^2 = 4\pi\left(\frac{1}{4}\right)= \pi$

Find the surface area of a hemisphere that has a radius of .

Explanation

In order to find the area of a hemisphere, which is just half a sphere, you will need to first find half the surface area of the sphere.

Recall how to find the surface area of a sphere:

$\text{Surface Area of Sphere}=4\pi r^2$ , where is the radius.

Now, since the sphere is cut in half, it also has a circle as its base.

Recall how to find the area of a circle:

$\text{Area of Circle}=\pi r^2$

Now add together half the surface area of a sphere with the area of the circular base to find the surface area of a hemisphere.

$\text{Surface Area of Hemisphere}=2\pi r^2+\pi r^2=3 \pi r^2$

Plug in the given radius to find the surface area.

$\text{Surface Area of Hemisphere}=3\pi (4)^2=150.80$

Make sure to round to places after the decimal.

If the radius of a sphere is , what is the surface area of the sphere?

$900\pi$

$225\pi$

$675\pi$

$13500\pi$

$300\pi$

Explanation

Write the equation for the surface area of a sphere.

$A=4\pi r^2$

Substitute the radius and find the area.

$A=4\pi (15)^2 = 4\pi(225)=900\pi$

Find the surface area of a sphere with a circumference of $\small \small 10\pi,cm$ .

$\small \small 100\pi,cm^2$

$\small \small 20\pi,cm^2$

$\small \small 400\pi,cm^2$

$\small \small 25\pi,cm^2$

$\small 200\pi,cm^2$

Explanation

The formula for the surface area of a sphere is simply

$\small A=4\pi r^2$

However, the problem is that we are given the circumference rather than the radius. Nonetheless, this isn't too big of an obstacle, as the formula for circumference in terms of radius is simply.

$\small C=2\pi r$

Substituting or value gives

$\small 10\pi=2\pi r$

Solving for the radius gives

$\small r=5$

We can then substitute this value into our formula for surface area.

$\small A=4\pi(5^2)$

$\small A=100\pi$

Therefore, our surface area is $\small 100\pi,cm^2$

If the radius of a sphere is , what is the sphere's surface area?

$4\pi:units$

$8\pi:units$

$\frac{4}{3}\pi:units$

$\frac{16}{9}\pi:units$

$2\pi:units$

Explanation

Write the formula for surface area of a sphere:

$A=4\pi r^2$

Plug in the value of radius and solve for the surface area:

$A=4\pi (1)^2 = 4\pi$

Find the surface area for a hemisphere that has a radius of $\frac{1}{2}$ .

Explanation

In order to find the area of a hemisphere, which is just half a sphere, you will need to first find half the surface area of the sphere.

Recall how to find the surface area of a sphere:

$\text{Surface Area of Sphere}=4\pi r^2$ , where is the radius.

Now, since the sphere is cut in half, it also has a circle as its base.

Recall how to find the area of a circle:

$\text{Area of Circle}=\pi r^2$

Now add together half the surface area of a sphere with the area of the circular base to find the surface area of a hemisphere.

$\text{Surface Area of Hemisphere}=2\pi r^2+\pi r^2=3 \pi r^2$

Plug in the given radius to find the surface area.

$\text{Surface Area of Hemisphere}=3\pi (\frac{1}{2})^2=2.36$

Make sure to round to places after the decimal.

The slant height of a cone is ; the diameter of its base is one-fifth its slant height. Give the surface area of the cone in terms of .

$\frac{11\pi L^{2}}{100}$

$\frac{6\pi L^{2}}{25}$

$\frac{ \pi L^{2}}{10}$

$\frac{ \pi L^{2}}{5}$

$\frac{ \pi L^{2}}{20}$

Explanation

The formula for the surface area of a cone with base of radius and slant height is

$A = \pi r^{2} + \pi r L$ .

The diameter of the base is $\frac{1}{5}L$ ; the radius is half this, so

$r = \frac{1}{2} \cdot \frac{1}{5}L= \frac{1}{10}L$

Substitute in the surface area formula:

$A = \pi \left ( \frac{1}{10}L \right ) ^{2} + \pi \left ( \frac{1}{10}L \right ) L$

$A = \frac{1}{100} \pi L^{2} + \frac{1}{10} \pi L^{2}$

$A = \frac{1}{100} \pi L^{2} + \frac{10}{100} \pi L^{2}$

$A = \frac{11}{100} \pi L^{2} = \frac{11\pi L^{2}}{100}$

The slant height of a cone is ; the diameter of its base is one-fifth its slant height. Give the surface area of the cone in terms of .

$\frac{11\pi L^{2}}{100}$

$\frac{6\pi L^{2}}{25}$

$\frac{ \pi L^{2}}{10}$

$\frac{ \pi L^{2}}{5}$

$\frac{ \pi L^{2}}{20}$

Explanation

The formula for the surface area of a cone with base of radius and slant height is

$A = \pi r^{2} + \pi r L$ .

The diameter of the base is $\frac{1}{5}L$ ; the radius is half this, so

$r = \frac{1}{2} \cdot \frac{1}{5}L= \frac{1}{10}L$

Substitute in the surface area formula:

$A = \pi \left ( \frac{1}{10}L \right ) ^{2} + \pi \left ( \frac{1}{10}L \right ) L$

$A = \frac{1}{100} \pi L^{2} + \frac{1}{10} \pi L^{2}$

$A = \frac{1}{100} \pi L^{2} + \frac{10}{100} \pi L^{2}$

$A = \frac{11}{100} \pi L^{2} = \frac{11\pi L^{2}}{100}$

Page 1 of 61

Return to subject

AI TutorYour personal study buddy

Questions of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

WorksheetsBuild custom practice quizzes

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Diagnostic TestsAssess your knowledge level

Practice TestsTest your skills with exam questions

GamesLearn through free games