All High School Math Resources
Example Questions
Example Question #12 : Polynomial Functions
Factor the polynomial if the expression is equal to zero when 
Knowing the zeroes makes it relatively easy to factor the polynomial.
The expression 
Now we need to check the answer.
We are able to get back to the original expression, meaning that the answer is 
Example Question #13 : Polynomial Functions
A polyomial with leading term 
Since 6 is a triple root, and the degree of the polynomial is 3, the polynomial is 
Example Question #1 : Express A Polynomial As A Product Of Linear Factors
A polyomial with leading term 
Since 5 is a single root and 7 is a double root, and the degree of the polynomial is 3, the polynomial is 
Example Question #3 : Understanding Zeros Of A Polynomial
What are the solutions to 
When we are looking for the solutions of a quadratic, or the zeroes, we are looking for the values of 
Then, we are looking for the values where each of these factors are equal to zero.

and 
Thus, these are our solutions.
Example Question #1 : Finding Zeros Of A Polynomial
Find the zeros of the following polynomial:
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:
Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for 

Since the function equals zero when 


Now we can factor the function this way:
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try 
When we factor using synthetic substitution for 
Using our quadratic factoring rules, we can factor completely:
Thus, the zeroes of 
Example Question #1 : Polynomials
Simplify the following polynomial:
To simplify the polynomial, begin by combining like terms:
Example Question #2 : Polynomials
Simplify the following polynomial function:
First, multiply the outside term with each term within the parentheses:
Rearranging the polynomial into fractional form, we get:
All High School Math Resources















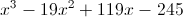

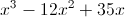

















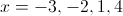
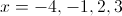


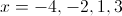

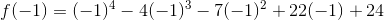





(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24))
![f(-2)=[(-2)+1][(-2)^{3}-5(-2)^{2}-2(-2)+24]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106228/gif.latex)
























