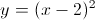Polynomial Functions
Help Questions
Math › Polynomial Functions
Which of the following is and accurate graph of 





Explanation
Remember 

Step 1, realize where 


C) The resulting point is 
Step 2, find simple points for 



The next resulting point; 


The next resulting point; 
Step 3, draw a curve through the considered points.
Find the zeros and asymptotes for

Zero: 
Zeros: 
Zero: 
Zeros: 
Zero: 
Explanation
To find the information we're looking for, we should factor this equation:
This means that it simplifies to 
When the equation is in the form of a fraction, to find the zero of the function we need to set the numerator equal to zero and solve for the variable.
To find the asymptote of an equation with a fraction we need to set the denominator of the fraction equal to zero and solve for the variable.
Therefore our equation has a zero at -3 and an asymptote at -2.
Find the roots of the function:
Explanation
Factor:
Double check by factoring:
Add together:
Therefore:
Solve this equation and check your answer:
No solution
Explanation
To solve this, first, find the common denominator. It is (n+1)(n-2). Multiply the entire equation by this:
Simplify to get:
Expand to get:
Move all terms to one side and combine to get:
Use the quadratic formula to get:
Find a fourth-degree polynomial whose zeroes are 
Explanation
This one is a bit of a journey. The expressions for the first two zeroes are easily calculated, 



Finally, we multiply together all of the parenthesized expressions, which multiplies out to
What transformations have been enacted upon 

vertical stretch by a factor of 4
horizontal compression by a factor of 2
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal stretch by a factor of 2
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal stretch by a factor of 2
horizontal translation 6 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 2
horizontal translation 6 units right
Explanation
First, we need to get this function into a more standard form.
Now we can see that while the function is being horizontally compressed by a factor of 2, it's being translated 3 units to the right, not 6. (It's also being vertically stretched by a factor of 4, of course.)
What transformations have been enacted upon 

vertical stretch by a factor of 4
horizontal compression by a factor of 2
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal stretch by a factor of 2
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal stretch by a factor of 2
horizontal translation 6 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 2
horizontal translation 6 units right
Explanation
First, we need to get this function into a more standard form.
Now we can see that while the function is being horizontally compressed by a factor of 2, it's being translated 3 units to the right, not 6. (It's also being vertically stretched by a factor of 4, of course.)
Divide the trinomial below by 
Explanation
We can accomplish this division by re-writing the problem as a fraction.
The denominator will distribute, allowing us to address each element separately.
Now we can cancel common factors to find our answer.
For the graph below, match the graph b with one of the following equations:




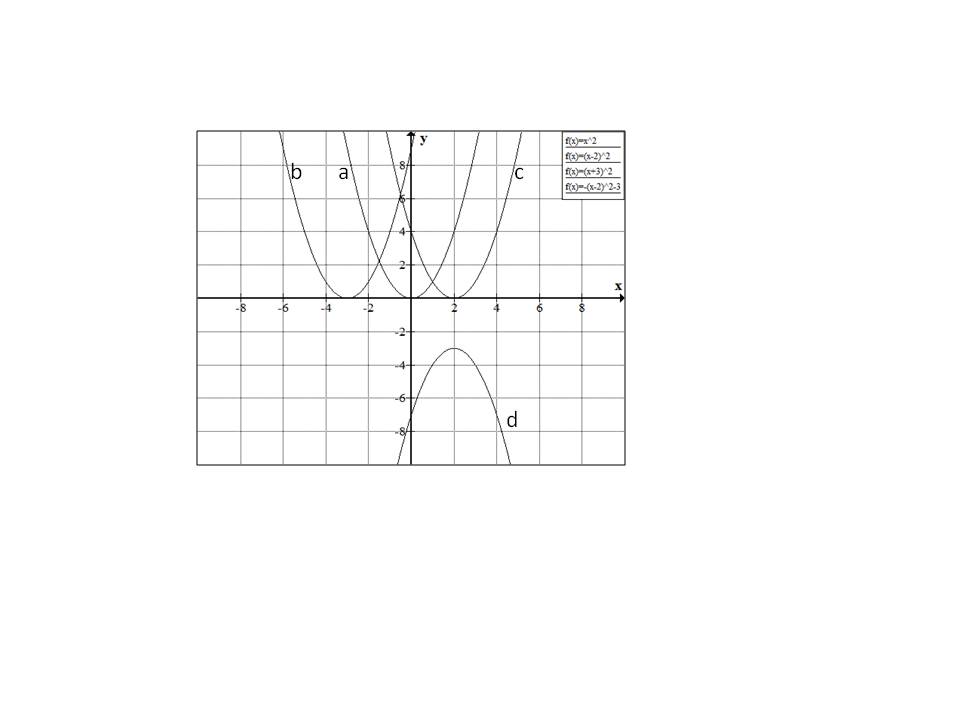




None of the above
Explanation
Starting with



Similarly 

Hence the correct answer is option 



























































![g(x)=4[2(x-3)]^{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/155687/gif.latex)