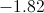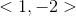Parametric, Polar, and Vector
Help Questions
Math › Parametric, Polar, and Vector
The polar coordinates of a point are 

Explanation
Given the polar coordinates 



The polar coordinates of a point are 

Explanation
Given the polar coordinates 



The polar coordinates of a point are 

Explanation
Given the polar coordinates 



The polar coordinates of a point are 

Explanation
Given the polar coordinates 



The polar coordinates of a point are 

Explanation
Given the polar coordinates 



The polar coordinates of a point are 

Explanation
Given the polar coordinates 



Given vector 


Explanation
To solve for 





Given vector 


Explanation
To solve for 





Given vector 


Explanation
To solve for 





Find the vector where its initial point is 

Explanation
We need to subtract the 

Initial pt:
Terminal pt:
Vector:
Vector: