All GRE Math Resources
Example Questions
Example Question #2 : Data Analysis
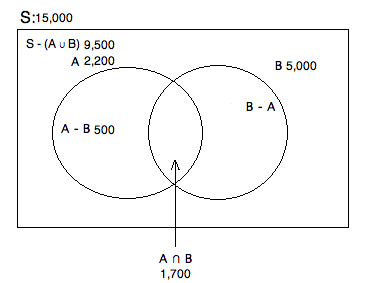
There are 15,000 students at college X. Of those students, 1,700 are taking both ethics and metaphysics this semester. There are 2,200 total students taking ethics. 9,500 students are taking neither of these classes. How many students are taking metaphysics this term?
1600
3300
None of the other answers.
5,000
3800
5,000
The easiest way to understand this problem is to draw a Venn Diagram:
S = Total number of students
A = Total students taking ethics
B = Total students taking metaphysics
A - B = Students taking only ethics
B - A = Students taking only metaphysics
A ∪ B = The total students taking either ethics or metaphysics
A ∩ B = The total students taking both ethics and metaphysics
We know there are 15,000 total and that 9,500 are taking neither class. Therefore, we know that 15,000 - 9,500 = 5,500 are taking at least one of the classes. Based on our prompt, we know that there are 1,700 taking both and that 2,200 are taking ethics. To fiind out how many are taking ONLY ethics, we have to subtract off the amount that are taking ethics and metaphysics. Hence, 2,200 - 1,700 = 500. Finally, if we know that there are 5,500 taking at at least one of these classes, we want to get rid of that portion taking ethics. This will leave us with those who are taking at least metaphysics (regardless of whether or not they are taking ethics): 5,500 - 500 = 5,000.
Example Question #1 : Venn Diagrams
In a class of 100 students, 43 play basketball and 37 play baseball. 9 students play both. How many students do not play either sport?
38
29
20
71
not enough information to answer the question
29
In order to determine how many students are not enrolled in a sport, we must first determine how many students are. The simplest way to do this is to begin by adding the students of both sports together.
43 + 37 = 80
But wait! 9 of those students are play both baseball and basketball. To avoid double counting these students, subtract 9 from the total.
80 – 9 = 71
Now we know 71 students play sports. If there are 100 students, all that's left to do is subtract.
100 – 71 = 29
29 students do not play basketball or baseball.
Example Question #1 : Venn Diagrams
There are 



You could represent this question in the following Venn Diagram:

We know that the two circles must contain a total of 
This is the simple answer to this question! You do not need to compute the overlap at all, as you are merely looking for the contents of the two circles.
All GRE Math Resources