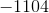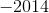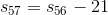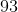All GRE Math Resources
Example Questions
Example Question #3 : Arithmetic Sequences
The sequence 
What is 
Begin by interpreting the general definition:
This means that every number in the sequence is five greater than the element preceding it. For instance:
It is easiest to count upwards:
Example Question #4 : Arithmetic Sequences
The sequence 
What is the value of 
For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:
This means that for every element in the list, each one is 
Now, notice that the first element is:
The second is:
The third could be represented as:
And so forth...
Now, notice that for the third element, there are only two instances of 
This value will always "lag behind" by one. Therefore, for the 
Example Question #3 : Nth Term Of An Arithmetic Sequence
The sequence 
What is the value of 
For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:
This means that for every element in the list, each one is 
Now, notice that the first element is:
The second is:
The third could be represented as:
And so forth...
Now, notice that for the third element, there are only two instances of 
This value will always "lag behind" by one. Therefore, for the 
All GRE Math Resources