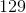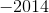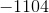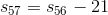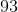All GRE Math Resources
Example Questions
Example Question #2 : Sequences
The first term in a sequence of integers is 2 and the second term is 10. All subsequent terms are the arithmetic mean of all of the preceding terms. What is the 39th term?
6
300
600
1200
5
6
The first term and second term average out to 6. So the third term is 6. Now add 6 to the preceding two terms and divide by 3 to get the average of the first three terms, which is the value of the 4th term. This, too, is 6 (18/3)—all terms after the 2nd are 6, including the 39th. Thus, the answer is 6.
Example Question #101 : Arithmetic
Consider the following sequence of integers:
5, 11, 23, 47
What is the 6th element in this sequence?
189
None of the other answers
191
95
93
191
First, consider the change in each element. Notice that in each case, a given element is twice the preceding one plus one:
11 = 2 * 5 + 1
23 = 11 * 2 + 1
47 = 23 * 2 + 1
To find the 6th element, continue following this:
The 5th: 47 * 2 + 1 = 95
The 6th: 95 * 2 + 1 = 191
Example Question #3 : Sequences
The sequence 




What is the value of the 
The first term of the sequence is 

Plugging these values into the given expression for the nth term gives us our answer.

Example Question #2 : Arithmetic Sequences
In a sequence of numbers, the first two values are 1 and 2. Each successive integer is calculated by adding the previous two and mutliplying that result by 3. What is fifth value in this sequence?
None of the other answers
Our sequence begins as 1, 2.
Element 3: (Element 1 + Element 2) * 3 = (1 + 2) * 3 = 3 * 3 = 9
Element 4: (Element 2 + Element 3) * 3 = (2 + 9) * 3 = 11 * 3 = 33
Element 5: (Element 3 + Element 4) * 3 = (9 + 33) * 3 = 42 * 3 = 126
Example Question #2 : Sequences
Let Z represent a sequence of numbers 

Let us first write the value of a consecutive term in a numerical format:
Consequently,
Using the first equation, we can define 

This allows us to rewrite
as
Rearrangement of terms allows us to solve for 
Now, using our second equation, we can find 
Example Question #101 : Arithmetic
The sequence 
What is 
Begin by interpreting the general definition:
This means that every number in the sequence is five greater than the element preceding it. For instance:
It is easiest to count upwards:
Example Question #3 : Sequences
The sequence 
What is the value of 
For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:
This means that for every element in the list, each one is 
Now, notice that the first element is:
The second is:
The third could be represented as:
And so forth...
Now, notice that for the third element, there are only two instances of 
This value will always "lag behind" by one. Therefore, for the 
Example Question #102 : Arithmetic
The sequence 
What is the value of 
For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:
This means that for every element in the list, each one is 
Now, notice that the first element is:
The second is:
The third could be represented as:
And so forth...
Now, notice that for the third element, there are only two instances of 
This value will always "lag behind" by one. Therefore, for the 
All GRE Math Resources