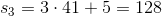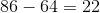All GRE Math Resources
Example Questions
Example Question #1 : Other Arithmetic Sequences
What is the sum of the odd integers 
None of the other answers
Do NOT try to add all of these. It is key that you notice the pattern. Begin by looking at the first and the last elements: 1 and 99. They add up to 100. Now, consider 3 and 97. Just as 1 + 99 = 100, 3 + 97 = 100. This holds true for the entire list. Therefore, it is crucial that we find the number of such pairings.
1, 3, 5, 7, and 9 are paired with 99, 97, 95, 93, and 91, respectively. Therefore, for each 10s digit, there are 5 pairings, or a total of 500. To get all the way through our numbers, you will have to repeat this process for the 10s, 20s, 30s, and 40s (all the way to 49 + 51 = 100).
Therefore, there are 500 (per pairing) * 5 pairings = 2500.
Example Question #2 : Sequences
A sequence is defined by the following formula:
What is the 4th element of this sequence?
With series, you can always "walk through" the values to find your answer. Based on our equation, we can rewrite 
You then continue for the third and the fourth element:
Example Question #94 : Arithmetic
What is the sum of the 40th and the 70th elements of the series defined as:
When you are asked to find elements in a series that are far into its iteration, you need to find the pattern. You absolutely cannot waste your time trying to calculate all of the values between 


For the third, you have:
Therefore, for the 40th and 70th elements, you will have:
The sum of these two elements is:
All GRE Math Resources