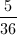All GRE Math Resources
Example Questions
Example Question #171 : Fractions
What is the result of adding 


Let us first get our value for the percentage of the first fraction. 20% of 2/7 is found by multiplying 2/7 by 2/10 (or, simplified, 1/5): (2/7) * (1/5) = (2/35)
Our addition is therefore (2/35) + (1/4). There are no common factors, so the least common denominator will be 35 * 4 or 140. Multiply the numerator and denominator of 2/35 by 4/4 and the numerator of 1/4 by 35/35.
This yields:
(8/140) + (35/140) = 43/140, which cannot be reduced.
Example Question #31 : Fractions
Reduce to simplest form:
Simplify expressions inside parentheses first: 
Now we have:
Add them by finding the common denominator (LCM of 4, 2, and 3 = 12) and then multiplying the top and bottom of each fraction by whichever factors are missing from this common denominator:
Example Question #32 : Fractions
Quantity A:
Quantity B:
Which of the following is true?
Quantity B is larger.
The two quantities are equal.
The relationship between the two quantities cannot be determined.
Quantity A is larger.
The two quantities are equal.
Start by looking at Quantity A. The common denominator for this expression is 
This is the same as:

This is the same as Quantity B. They are equal!
Example Question #3 : Operations
Solve for 
Begin by isolating the 
Now, the common denominator of these two fractions is 


Now, you can subtract the left values:
Now, multiply both sides by 
Example Question #4 : Operations
Simplify:
Just like adding fractions, when you subtract fractions, you need to find a common denominator. For 


Which is the same as...
Now, you can subtract the numerators and retain the denominator:
Example Question #1 : How To Subtract Fractions
Which of the following is true?
Quantity A:
Quantity B:
The relationship between the quantities cannot be determined.
Quantity A is larger.
The two quantities are equal.
Quantity B is larger.
Quantity A is larger.
First, consider each quantity separately.
Quantity A
These two fractions do not have a common factor. Their common denominator is 
This is the same as:
Quantity B
The common denominator of these two values is 
This is the same as:
Since Quantity A is larger than 

Example Question #1 : How To Multiply Fractions
There are 340 students at Saint Louis High School in the graduating senior class. Of these students, 9/10 are going to college. Of those going to college, 2/5 are going to Saint Louis University. How many students are going to Saint Louis University?
306
The answer cannot be determined from the given information.
122
103
136
122
122 students are going to Saint Louis University. To answer this question, the following equation can be used: 340*(9/10)*(2/5) . This is then rounded down to 122 students attending Saint Louis University.
Example Question #1 : How To Multiply Fractions
If 


The least common multiple of 4 and 6 is 12.
So we know if 



So then it follows that


Example Question #2 : How To Multiply Fractions
If 


Example Question #461 : Arithmetic
At a certain company, one quarter of the employees take the bus to work and one third drive. Of the remaining employees, half walk, one third ride a bike, and the rest take the subway.
Out of the total number of employees, what fraction ride a bike to work?
First we want to find the fraction of employees that neither take the bus nor drive, so we’ll add the fractions that do take the bus or drive and subtract that result from the total.
Bus:
Drive:
Remaining:
Now we need the fraction representing one third of these remaining employees (the fraction that ride a bike). Since "of " means multiply, we'll multiply.
All GRE Math Resources