All GMAT Math Resources
Example Questions
Example Question #1 : Calculating The Perimeter Of An Acute / Obtuse Triangle
A triangle has 2 sides length 5 and 12. Which of the following could be the perimeter of the triangle?
I. 20
II. 25
III. 30
I and II only
III only
I only
II and III only.
All 3 are possible.
II and III only.
For a triangle, the sum of the two shortest sides must be greater than that of the longest. We are given two sides as 5 and 12. Our third side must be greater than 7, since if it were smaller than that we would have 


Thus our perimeter will be between 

Example Question #2 : Calculating The Perimeter Of An Acute / Obtuse Triangle

Triangle 


To calculate the perimeter, we simply need to add the three sides of the triangle.
Therefore, the perimeter is 
Example Question #3 : Acute / Obtuse Triangles

Triangle 





Since BD is the height of triangle ABC, we can apply the Pythagorean Theorem to, let's say, triangle DBC and 
Since the basis of the height is at the midpoint of AC, it follows that triangle ABC, is an isoceles triangle.
We can find the perimeter by multiplying BC by 2 and add the basis of the triangle AC, which has length of 
The final answer is therefore 
Example Question #1 : Acute / Obtuse Triangles
An acute triangle has side lengths of 


For any given triangle, the perimeter 




Example Question #1 : Acute / Obtuse Triangles
An acute triangle has side lengths of 


For any given triangle, the perimeter 




Example Question #1 : Acute / Obtuse Triangles
An acute triangle has side lengths of 


For any given triangle, the perimeter 




Example Question #1 : Acute / Obtuse Triangles
Is it true that 
Suppose you want to answer this question, and you know that 

None of these statements would be sufficient to answer the question.
If you know either that 

If you know that 

If you also know that 
Example Question #1 : Calculating Whether Acute / Obtuse Triangles Are Congruent
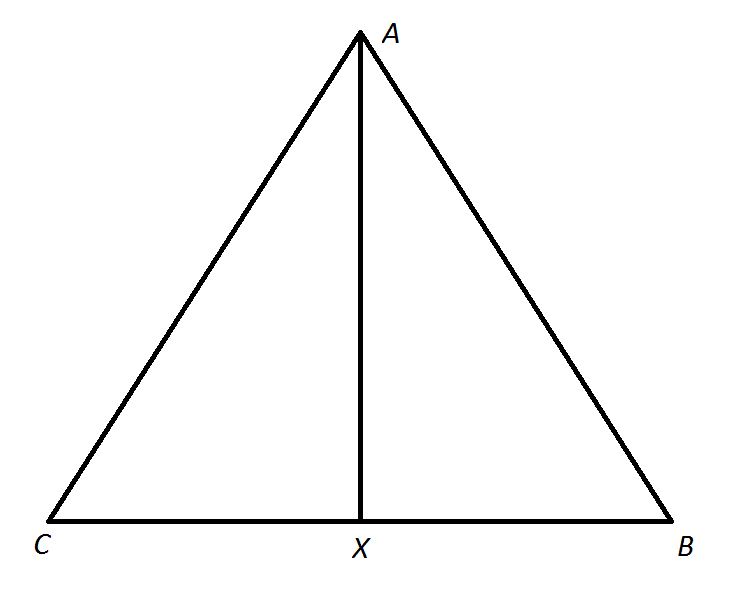
Note: Figure NOT drawn to scale
Refer to the above diagram. Which of the following statements is NOT a consequence of the fact that 






We use the congruence of corresponding sides and angles of congruent triangles to prove four of these statements:








However, nothing in this congruence proves that 


Example Question #331 : Geometry
Which of the following cannot be the measure of a base angle of an isosceles triangle?
Each of the other choices can be the measure of a base angle of an isosceles triangle.
An isosceles triangle has two congruent angles by the Isosceles Triangle Theorem; these are the base angles. Since at least two angles of any triangle must be acute, a base angle must be acute - that is, it must measure under 

Example Question #332 : Geometry
Let the three interior angles of a triangle measure 

The triangle is scalene and acute.
The triangle is scalene and obtuse.
The triangle is isosceles and acute.
The triangle is scalene and right.
The triangle is isosceles and obtuse.
The triangle is isosceles and acute.
If these are the measures of the interior angles of a triangle, then they total 

One angle measures 
All three angles measure less than 
All GMAT Math Resources














































