Circles
Help Questions
GMAT Quantitative › Circles
The arc 



Explanation
A circle can be divided into 

If the 



A 

Explanation
A 



The radius of a circle is its circumference divided by 
What is the area of a circle with a diameter of 
Explanation
The area 




If 
Then, solving for 
The chord of a 

Explanation
The radius 

The circle, the central angle, and the chord are shown below:

By way of the Isosceles Triangle Theorem, 

The arc 



Explanation
The figure referenced is below.
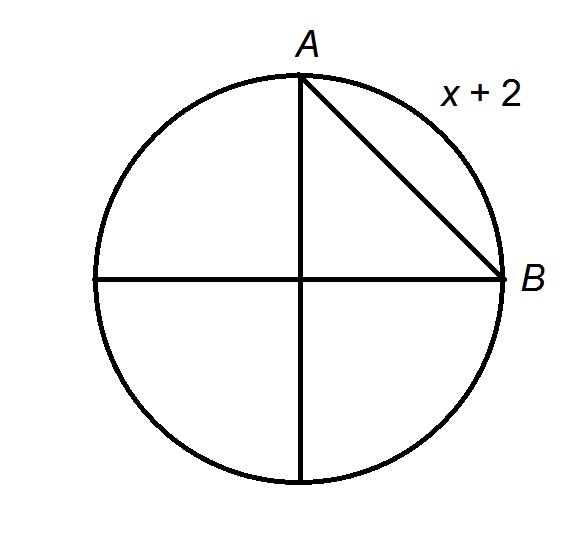
The arc is 

The radius is this circumference divided by 

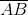


Calculate the length of a chord in a circle with a radius of 

Explanation
We are given the radius of the circle and the perpendicular distance from its center to the chord, which is all we need to calculate the length of the chord. Using the formula for chord length that involves these two quantities, we find the solution as follows, where 


What percentage of a circle is a sector if the angle of the sector is 
Explanation
The full measure of a circle is 





The circle in the above diagram has center 
Statement 1: Arc 

Statement 2: Arc 

BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
Explanation
Assume Statement 1 alone. Since the circumference of the circle is not given, it cannot be determined what part of the circle 
Now assume both statements are true. Then the length of semicircle 







A given circle has an area of 
Not enough information provided
Explanation
The area 




Given 




The points 

To the nearest hundreth, what is the length of the radius of circle Q?
Explanation
To begin this problem, we need to recognize that the distance between points L and K is our diameter. Segment LK passes from one point on circle Q through the center, to another point on circle Q. Sounds like a diameter to me! Use distance formula to find the length of LK.
Plug in our points and simplify:
Now, don't be fooled into choosing 13.15. That is our diameter, so our radius will be half of 13.15, or 6.575. This rounds to 6.58


























































