Circles
Help Questions
GMAT Quantitative › Circles
The chord of a 

Explanation
The radius 

The circle, the central angle, and the chord are shown below:

By way of the Isosceles Triangle Theorem, 

The arc 



Explanation
The figure referenced is below.
The arc is 

The radius is this circumference divided by 

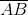


Calculate the length of a chord in a circle with a radius of 

Explanation
We are given the radius of the circle and the perpendicular distance from its center to the chord, which is all we need to calculate the length of the chord. Using the formula for chord length that involves these two quantities, we find the solution as follows, where 


A given circle has an area of 
Not enough information provided
Explanation
The area 




Given 




Two circles are constructed; one is inscribed inside a given regular hexagon, and the other is circumscribed about the same hexagon.
The inscribed circle has circumference 
Explanation
Examine the diagram below, which shows the hexagon, segments from its center to a vertex and the midpoint of a side, and the two circles.

Note that the segment from the center of the hexagon to the midpoint of a side is a radius of the inscribed circle, and the segment from the center to a vertex is a radius of the circumscribed circle. The two segments and half a side of the hexagon can be proved to form a 30-60-90 triangle.
The inscribed circle has circumference 
By the 30-60-90 Theorem, the length of the shorter leg is this length divided by 


The area of the circumscribed circle can now be calculated:
What is the arc length for a sector with a central angle of 

Explanation
Using the formula for arc length, we can plug in the given angle and radius to calculate the length of the arc that subtends the central angle of the sector. The angle, however, must be in radians, so we make sure to convert degrees accordingly by multiplying the given angle by 
Two circles are constructed; one is inscribed inside a given equilateral triangle, and the other is circumscribed about the same triangle.
The inscribed circle has circumference 
Explanation
Examine the diagram below, which shows the triangle, its three altitudes, and the two circles.

The three altitudes of an equilateral triangle divide one another into two segments each, the longer of which is twice the length of the shorter. The length of each of the longer segments is the radius of the circumscribed circle, and the length of each of the shorter segments is the radius of the inscribed circle. Therefore, the circumscribed circle has twice the radius of the inscribed circle.
The inscribed circle has circumference 
The circumscribed circle has radius twice this, or 20, so its area is
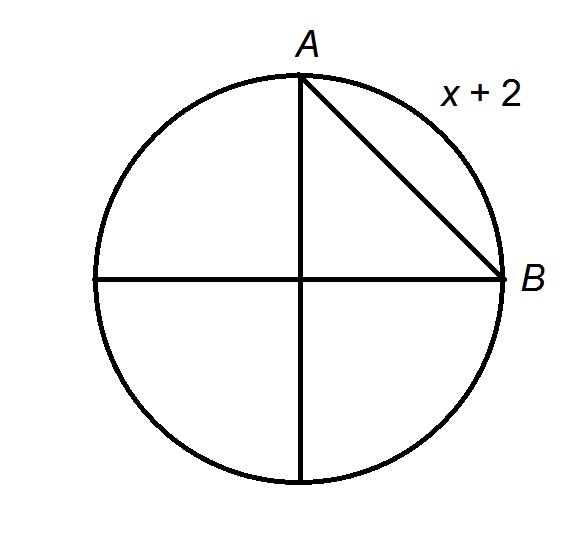
The arc 




Explanation
Examine the figure below, which shows the arc and chord in question.

If we extend the figure to depict the circle as the composite of four quarter-circles, each a 



is a diameter of this circle. The circumference is 

Since a 

Two circles are constructed; one is inscribed inside a given square, and the other is circumscribed about the same square.
The inscribed circle has circumference 
Explanation
Examine the diagram below, which shows the square, segments from its center to a vertex and the midpoint of a side, and the two circles.

Note that the segment from the center of the square to the midpoint of a side is a radius of the inscribed circle, and the segment from the center to a vertex is a radius of the circumscribed circle. The two segments and half a side of the square form a 45-45-90 triangle, so by the 45-45-90 Theorem, the radius of the circumscribed circle is 
The inscribed circle has circumference 
The circumscribed circle has radius 

Two circles are constructed; one is inscribed inside a given square, and the other is circumscribed about the same square.
The circumscribed circle has circumference 
The correct answer is not among the other responses.
Explanation
Examine the diagram below, which shows the square, segments from its center to a vertex and the midpoint of a side, and the two circles.

Note that the segment from the center of the square to the midpoint of a side is a radius of the inscribed circle, and the segment from the center to a vertex is a radius of the circumscribed circle. The two radii and half a side of the square form a 45-45-90 Triangle, so by the 45-45-90 Theorem, the radius of the inscribed circle is equal to that of the circumscribed circle divided by 
The inscribed circle has circumference 
Divide this by 
The circumscribed circle has area
































































