All GED Math Resources
Example Questions
Example Question #31 : Probability
A bag contains the following:
- 2 pencils
- 4 pens
- 1 marker
Find the probability of grabbing a marker.
To find the probability of an event, we will use the following formula:
Now, given the event of grabbing a marker, we can calculate the following:
because there is 1 marker we can grab.
We can also calculate the following:
because there are 7 objects we could potentially grab:
- 2 pencils
- 4 pens
- 1 marker
Now, we can substitute. We get
Therefore, the probability of grabbing a marker from the bag is 
Example Question #1851 : Ged Math
Billy flips a fair coin three times. His results were three tails. Billy then flipped the coin three times again and was shocked to see the results were also three tails! What is the probability that Billy flipped the coin 6 times, and all trials are tails?
Every result for a fair coin is independent of the previous trials.
The probability of landing heads or tails is 
For the coin to land on tails six consecutive times,
The answer is:
Example Question #1851 : Ged Math
A classroom contains the following:
- 12 boys
- 14 girls
Find the probability the teacher calls on a girl.
To find the probability of an event, we will use the following formula:
Given the event of the teacher calling on a girl, we can calculate the following:
because there are 14 girl in the class.
We can also calculate the following:
because there are 26 total students in the class the teacher could potentially call on:
- 12 boys
- 14 girls
So, we substitute. We get
Therefore, the probability that the teacher calls on a girl is
Example Question #32 : Probability
A board game uses a six sided die, and a spinner that is split into quarters with the colors red, blue, yellow, and green. What is the probability of rolling a 

Start by figuring out the probability of rolling a 



Next, figure out the probability of spinning green. Since the spinner is divided equally into quarters, the probability of spinning green is 
Because the question asks about the probability of both events happening, you will need to multiply the two probabilities together.
Example Question #31 : Probability
For a certain game, players will need to spin a spinner divided into equal sixths and numbered from 



Start by finding the probability of spinning an even number. We have 


Next, determine the probability of rolling a 



Since the question asks about the probability of both events happening, we will need to multiply the two probabilities.
Example Question #31 : Statistics
At a certain carnival game, players must toss beanbags into a small colored circle within a square playing field, as shown by the figure below.

The length of one side of the playing field is 
Recall the definition of a probability:
Now, the desired outcome for this scenario is the beanbag landing in the circle. Thus, we can use the area of the circle as the desired outcome. In addition, the total possible outcomes can then be represented by the area of the entire square playing field.
Start by finding the area of the playing field. Recall how to find the area of a square:
Plug in the given side length of the square.
Next, find the area of the circle.
Since the question informs us that the diameter of the circle is one-fourth that of the side of the square playing field, the diameter of the circle must be 

Recall how to find the area of the circle.
Plug in the given radius to find the area of the circle.
Now that we have both areas, we can write probability:
Example Question #1852 : Ged Math
A class of 

If two students are selected at random from this class one after another without replacement, what is the probability that the first student selected will have 

Recall how to find the probability of an event:
Since there are 


Now, since we are selecting students without replacement, this means that the total number of students to choose from when it's time to select the second student is 


Since the question wants to know the probability of both events happening, we will multiply the probabilities together:
Example Question #1851 : Ged Math
If you have a standard, six-sided die, what is the probability of rolling two numbers greater than 3 on two separate rolls?
If you have a standard, six-sided die, what is the probability of rolling two numbers greater than 3 on two separate rolls?
We need to find the probability of two independent events. To do so, we need to find the probability of each event and multiply them.
There are three numbers on a six-sided die that are greater than 3 (4,5,and 6).
Thus, our probability of each event is
But, we want the probability of doing this twice, so we need to multiply our probabilities.
So, our answer is
Example Question #1853 : Ged Math
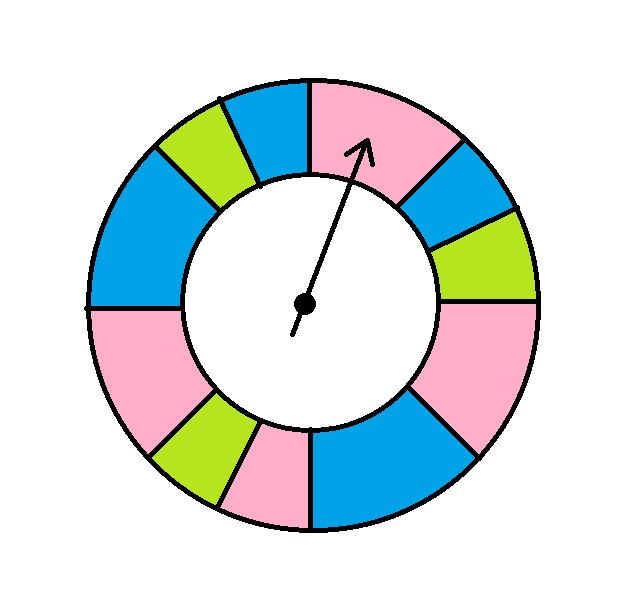
If the arrow in the above spinner is spun, what is the probability that it will land in a green region?
Each of the larger regions is one-eighth of the ring; each of the smaller regions is one-sixteenth of the ring. There are three small green regions and no large green regions, so the green portion of the ring is
of the ring. This is the probability that the arrow will land in a green region.
Example Question #31 : Statistics
In order to win a carnival game, a player must roll an even number on a fair six-sided die, then spin have a spinner land on the blue portion. The spinner is evenly divided into five sections with the following colors: red, blue, yellow, green, and purple. What is the probability of winning this game?
Recall what a probability is:
For the die, we can find the probability of rolling an even number:
Next, for the spinner, we can find the probability of landing on blue:
Since we want the probability of both evens happening, we will need to multiply the individual probabilities together:
All GED Math Resources

















































































