All GED Math Resources
Example Questions
Example Question #1 : Squares, Rectangles, And Parallelograms

Note: Figure NOT drawn to scale
Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in brown) six feet wide throughout. What is the perimeter of the garden?
The inner rectangle, which represents the garden, has length and width 


Example Question #2 : Squares, Rectangles, And Parallelograms
Which of the following can be the sidelengths of a rhombus?
The four sides of a rhombus have equal length, so we can eliminate three choices by demonstrating that at least two sidelengths are not equal.

1,000 meters is, by definition, equal to 1 kilometer, not 0.1 kilometers. Therefore,
and this choice is incorrect.

1 mile is, by definition, equal to 5,280 feet, not 1,760 feet. Therefore,
and this choice is incorrect.
By definition, 1 decimeter, not 0.1 decimeter, is equal to 1 meter. Therefore,
and this choice is incorrect.




All four sides have equal length so this is the rhombus. This is the correct choice.
Example Question #3 : Perimeter And Sides Of Quadrilaterals

Identify the above polygon.
Pentagon
Trapezoid
Rhombus
Hexagon
Hexagon
A polygon with six sides is called a hexagon.
Example Question #1 : Squares, Rectangles, And Parallelograms

Refer to the above three figures. All parallel sides are so indicated.
Which of the figures can be called a quadrilateral?
Figure C only
Figures B and C only
Figures A, B, and C
Figures A and B only
Figures A, B, and C
By definition, any polygon with four sides is called a quadrilateral. All three figures fit this description.
Example Question #1 : Perimeter And Sides Of Quadrilaterals

Refer to the above diagram. Parallel sides are so indicated.
Identify the above polygon.
Parallelogram
Hexagon
Trapezoid
Pentagon
Trapezoid
A four-sided figure, or quadrilateral, with one pair of parallel sides and its other sides nonparallel is called a trapezoid.
Example Question #6 : Perimeter And Sides Of Quadrilaterals
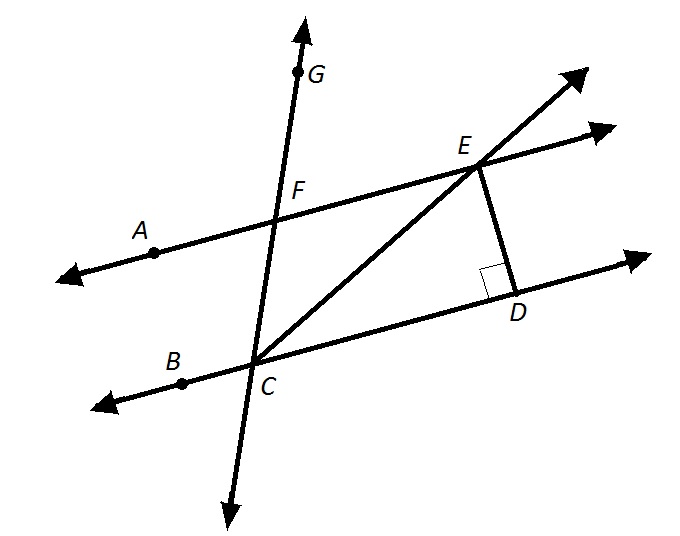
Refer to the above figure. You are given that 

Which of the following words accurately describes Polygon 
Pentagon
Parallelogram
Trapezoid
Hexagon
Trapezoid
Polygon 






The quadrilateral has one pair of parallel sides, and the other two sides are not parallel. Therefore, it is a trapezoid.
Example Question #5 : Squares, Rectangles, And Parallelograms

Refer to the above three figures. All parallel sides are so indicated.
Which of the figures can be called a parallelogram?
Figure C only
Figures A and B only
Figure B only
Figures A, B, and C
Figures A and B only
A parallelogram, by definition, has two pairs of parallel sides. Figures A and B fit that criterion, but Figure C does not.
Example Question #6 : Squares, Rectangles, And Parallelograms

Note: Figure NOT drawn to scale.
Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in brown). The dirt path is 
The length of the garden is 

The width of the garden is 

The perimeter is twice the sum of the two:
Example Question #4 : Squares, Rectangles, And Parallelograms

Note: Figure NOT drawn to scale.
Quadrilateral 
The four sides of a rhombus are congruent. Also, the diagonals of a rhombus are perpendicular bisectors to each other, so the four triangles they form are right triangles. Therefore, the Pythagorean theorem can be used to determine the common sidelength of Quadrilateral 
We focus on 
By the Pythagorean Theorem,
13 is the common length of the four sides of Quadrilateral 

Example Question #10 : Perimeter And Sides Of Quadrilaterals

Note: Figure NOT drawn to scale
Give the ratio of the perimeter of Rectangle 

The perimeter of Rectangle 

Opposite sides of a rectangle are congruent, so
and

The perimeter of Rectangle 

Opposite sides of a rectangle are congruent, so


and

The ratio of the perimeters is

All GED Math Resources






































