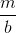All Calculus 1 Resources
Example Questions
Example Question #1 : How To Find Constant Of Proportionality Of Rate
Suppose a blood cell increases proportionally to the present amount. If there were 


The population size 

where 
At the start, there were 30 blood cells.
Substitute this value into the given formula.
After 2 hours, 45 blood cells were present. Write this in mathematical form.
Substitute this into 

Example Question #2 : How To Find Constant Of Proportionality Of Rate
Given any linear function 
Direct constant of proportionality for any given function y, between any x values, is given by


In the case of a linear function

Therefore, the constant of proportionality is
Example Question #1 : Constant Of Proportionality
Find the direct constant of proportionality of 


To determine the direct constant of proportionality, we determine the rate of change from 


Rate of change is determined by

In our case, 



Example Question #1 : Constant Of Proportionality
Find the direct constant of proportionality 



Direct constant of proportionality 

Since 
Example Question #2 : How To Find Constant Of Proportionality Of Rate
Suppose a population of bacteria increases from 


None of these
The equation for population growth is given by 






Now that we solved for 


Example Question #1 : How To Find Constant Of Proportionality Of Rate
A population of deer grew from 50 to 200 in 7 years. What is the growth constant for this population?
None of these
The equation for population growth is given by 





Now that we have solved for 

Example Question #901 : Rate
A population of mice has 200 mice. After 6 weeks, there are 1600 mice in the population. What is the constant of growth?
The equation for population growth is given by 






Now that we have 


Example Question #3721 : Calculus
Find the direct constant of proportionality 




Direct constant of proportionality 





Since 

Example Question #3 : How To Find Constant Of Proportionality Of Rate
The rate of decrease of the dwindling wolf population of Zion National Park is proportional to the population. The population decreased by 7 percent between 2009 and 2011. What is the constant of proportionality?
We're told that the rate of growth of the population is proportional to the population itself, meaning that this problem deals with exponential growth/decay. The population can be modeled thusly:
Where 

Since the population decreased by 7 percent between 2009 and 2011, we can solve for this constant of proportionality:
Example Question #3 : Constant Of Proportionality
The rate of growth of the Martian Transgalactic Constituency is proportional to the population. The population increased by 23 percent between 2530 and 2534 AD. What is the constant of proportionality?
We're told that the rate of growth of the population is proportional to the population itself, meaning that this problem deals with exponential growth/decay. The population can be modeled thusly:
Where 

Since the population increased by 23 percent between 2530 and 2534 AD, we can solve for this constant of proportionality:
Certified Tutor
Certified Tutor
All Calculus 1 Resources