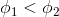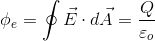Electricity
Help Questions
AP Physics C: Electricity and Magnetism › Electricity
A proton moves in a straight line for a distance of 

The charge of a proton is 
Explanation
Potential difference is given by the change in voltage
Work done by an electric field is equal to the product of the electric force and the distance travelled. Electric force is equal to the product of the charge and the electric field strength.
The charges cancel, and we are able to solve for the potential difference.
A proton moves in a straight line for a distance of 

The charge of a proton is 
Explanation
Potential difference is given by the change in voltage
Work done by an electric field is equal to the product of the electric force and the distance travelled. Electric force is equal to the product of the charge and the electric field strength.
The charges cancel, and we are able to solve for the potential difference.
A charge, 



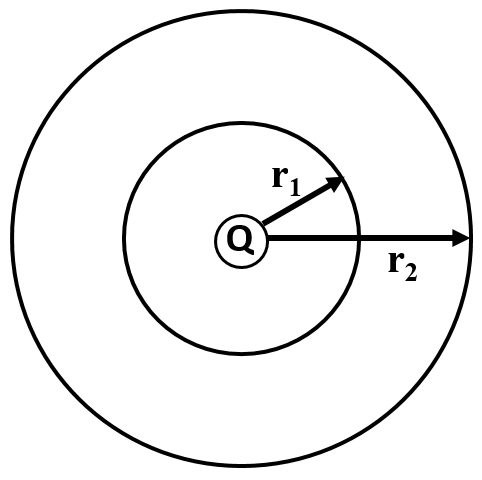
Which is the correct relationship between the electric flux passing through the two spherical surfaces around the point charge?
Explanation
Electric flux is given by either side of the equation of Gauss's Law:
Since the charge is the same for both spherical surfaces, even though these surfaces are of different radii, the amounts of electric flux passing through each surface is the same.
A charge, 




Which is the correct relationship between the electric flux passing through the two spherical surfaces around the point charge?
Explanation
Electric flux is given by either side of the equation of Gauss's Law:
Since the charge is the same for both spherical surfaces, even though these surfaces are of different radii, the amounts of electric flux passing through each surface is the same.
You are standing on top of a very large positively charged metal plate with a surface charge of 
Assuming that the plate is infinitely large and your mass is 
Explanation
Consider the forces that are acting on you. There is the downward (negative direction) force of gravity, 



For plates that are charged, know that 
Knowing this, the force equation becomes 
Solve for 
Now we can plug in our given values, and solve for the charge.
Two capacitors are in parallel, with capacitance values of 

Explanation
The equivalent capacitance for capacitors in parallel is the sum of the individual capacitance values.
Using the values given in the question, we can find the equivalent capacitance.
You are standing on top of a very large positively charged metal plate with a surface charge of 
Assuming that the plate is infinitely large and your mass is 
Explanation
Consider the forces that are acting on you. There is the downward (negative direction) force of gravity, 



For plates that are charged, know that 
Knowing this, the force equation becomes 
Solve for 
Now we can plug in our given values, and solve for the charge.
Two point charges, 



The values of the charges are:
The distance is 4.0cm. The point 

What is the magnitude and direction of the net electric field at point 
Explanation
At point 


At point P, the electric field due to Q2 points away from Q2 with a magnitude given by
The addition of these two vectors, both pointing in the same direction, results in a net electric field vector of magnitude 152000 volts per meter, pointing toward 
Two capacitors are in parallel, with capacitance values of 

Explanation
The equivalent capacitance for capacitors in parallel is the sum of the individual capacitance values.
Using the values given in the question, we can find the equivalent capacitance.
Two point charges, 



The values of the charges are:
The distance is 4.0cm. The point 

What is the magnitude and direction of the net electric field at point 
Explanation
At point 


At point P, the electric field due to Q2 points away from Q2 with a magnitude given by
The addition of these two vectors, both pointing in the same direction, results in a net electric field vector of magnitude 152000 volts per meter, pointing toward