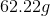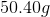All AP Physics 2 Resources
Example Questions
Example Question #1 : Heat Transfer And Thermal Equilibrium



There is not enough information to determine the rod's mass
The relevant equation for this problem is called the specific heat capacity equation:
In this equation, 




To find the mass of the rod when given the energy, specific heat, and change in temperature, we can rearrange the equation to this:
Now, we can plug in our numbers and solve:
Example Question #1 : Thermodynamics
Which of the following best defines the zeroth law of thermodynamics in variable form?
The zeroth law of thermodynamics states that if an object X is in thermal equilibrium with object Y, and object Y also in thermal equilibrium with object Z, then object X must also be in thermal equilibrium with object Z.




The best choice is:
Example Question #1 : Heat Transfer And Thermal Equilibrium
You have 


There's not enough information to determine the temperature change
The equation for temperature change given applied heat is






Rearranging to find the change in temperature:
Now, we can plug in our numbers.
Therefore, the water changed by about 
Example Question #2 : Heat Transfer And Thermal Equilibrium
You have 


There is not enough information to determine the specific heat of this metal
To find the specific heat of an unknown material given temperature change, mass, and energy applied, we use the following equation:
Plug in known values and solve.
Example Question #1 : Heat Transfer And Thermal Equilibrium
How much energy does it take to raise 

The equation that is needed is:
Plug in known values and solve.
Example Question #3 : Heat Transfer And Thermal Equilibrium
The heat capacity for any given material is defined as the amount of heat that must be added to that material in order to increase its temperature by 
How would the heat capacity for a material at constant volume differ from the heat capacity for that same material at constant pressure?
The heat capacity at constant volume is equal to the heat capacity at constant pressure
There is no way to tell; the relative values of the constant volume and constant pressure heat capacities depends on the material under consideration
The heat capacity at constant pressure is greater than the heat capacity at constant volume
The heat capacity at constant volume is greater than the heat capacity at constant pressure
The heat capacity at constant pressure is greater than the heat capacity at constant volume
In this question, we're presented with the definition of heat capacity. We're also told that the heat capacity for any given material can be measured at 1) constant volume, or 2) constant pressure. We're being asked to determine whether the constant volume heat capacity is greater than, less than, or equal to the constant pressure heat capacity for the same material.
First, let's revisit the definition of heat capacity. It is the amount of heat that must be added to a material to raise the temperature of that material by 
Next, let's consider what is happening as we add heat to a material at constant volume. When the volume of a material is held constant, that means that it is prevented from expanding as heat is added. Thus, all of the heat being added is resulting directly in an increase in the average kinetic energy of the particles that make up that material. In other words, all of the heat being added results in a temperature increase.
Let's now consider what happens when heat is added to a material at constant pressure. In this situation, the material is allowed to expand as heat is added to it (because volume is not being held constant). Therefore, when heat is added to the material, some of the heat will result in an increased temperature, but some of the heat will also result in an expansion of the material. The consequence of this is that in order to increase the temperature of the material by a given amount at constant pressure, it will require more heat energy than at constant volume.
Again, the main point of this is as follows:
- Constant volume - all of the added heat results in increased temperature
- Constant pressure - some of the added heat results in increased temperature and some of the added heat results in expansion
Since only a fraction of the heat being added at constant pressure will actually result in a temperature increase, we'll have to add more heat in order to increase its temperature by a given amount, when compared to constant volume conditions.
Example Question #4 : Heat Transfer And Thermal Equilibrium




Since the two gases are in an isolated system, we know that the heat lost by one is equal to the heat gained by the other. Furthermore, we know that the two gases will be in thermal equilibrium when they have the same temperature, which will be some value in between their two initial values. Since methanol is at a higher temperature, we can say that it will loose heat and ethanol will gain that same amount of heat:
Substituting in expressions for each of these, we get:
Where the final temperature is equal for both gases:
Now we simply need to rearrange for the final temperature:
We have all of these values, so time to plug and chug:
Example Question #13 : Thermodynamics
Suppose that a copper bar 



To find out how much the bar will change in length, we'll need to use the equation for thermal expansion, which is as follows:
If we plug in the values that we know, we can solve for the change in length of the bar.
Now, we just need to add this value to the original length of the bar, and we will have our final answer.
Example Question #1 : Heat Transfer And Thermal Equilibrium
Ana is holding onto an ice cube. Why does it melt in her hand?
All of these
The cold leaves the ice cube
The ice cube gave off energy to her hand
Her hand took energy from the ice cube
The heat from her hand warms it
The heat from her hand warms it
According to the second law of thermodynamics, heat flows from hot to cold. Thus, the heat from her hand flows into the ice cube, causing it to melt.
Example Question #15 : Thermodynamics
An ideal heat engine uses the atmosphere as a low temperature reservoir and boiling water as a hot temperature reservoir. Water boils at 



Equally efficient
Not enough information.



The efficiency of an ideal heat engine is given by:




The denominator does not change if the temperature is hot or cold, so we need only consider the numerator. Let's compare both calculations:
Hot Day:
Cold Day:
Comparing these two efficiencies, we see that the cold day is roughly 
All AP Physics 2 Resources