All AP Calculus AB Resources
Example Questions
Example Question #46 : Derivative As A Function
Find the relative maxima of the following function:
The function has no relative maxima
The function has no relative maxima
To determine the values at which the function has a relative maximum, we must determine the intervals on which the function's first derivative changes from positive to negative.
The first derivative of the function is equal to
and was found using the following rules:


Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is positive, and on the second interval, the first derivative is positive. Because the first derivative never changed sign, the function has no relative extrema.
Example Question #47 : Derivative As A Function
Determine the intervals on which the function is decreasing:
The function is never decreasing
To determine the intervals on which the function is decreasing, we must determine the intervals on which the function's first derivative is negative.
The first derivative of the function is equal to
and was found using the following rules:


Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is negative, and on the second interval, the first derivative is negative as well. Thus, the function is decreasing on its entire domain, 
Example Question #48 : Derivative As A Function
Find the intervals on which the function is decreasing:
To determine the intervals on which the function is decreasing, we must determine the intervals on which the function's first derivative is negative.
The first derivative of the function is equal to
and was found using the following rules:

Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is negative, on the second interval, the first derivative is positive, on the third interval, the first derivative is negative, and on the fourth interval, the first derivative is positive. Thus, the function is decreasing on 
Example Question #41 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'
Find the intervals on which the function is increasing:
The function is never increasing
To determine the intervals on which the function is increasing, we must determine the intervals on which the function's first derivative is positive.
The first derivative of the function is equal to
and was found using the following rule:
Next, we must find the critical values, at which the first derivative is equal to zero:
Notice that the critical values are bounded by the interval given in the problem statement.
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is negative, on the second interval, the first derivative is positive, and on the third interval, the first derivative is negative. Thus, the function is increasing on 
Example Question #42 : Derivative As A Function
Solve the separable differential equation:
To solve the separable differential equation, we must separate x and y to the same sides as their respective derivatives:
Next, we integrate both sides:
The integrals were solved using the following rule:
The two constants of integration were combined to make a single one.
Now, we use algebra to solve for y:
Example Question #41 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'
Determine the intervals on which the function is increasing:
To determine the intervals on which the function is increasing, we must determine the intervals on which the function's first derivative is positive.
The first derivative of the function is equal to
and was found using the following rules:


Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative, nor is it defined at 
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is positive, on the second and third intervals, the first derivative is negative, and on the fourth interval, the first derivative is positive. Thus, the function is increasing on 
Example Question #42 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'
Which function has a positive slope at x=5?
None of the other answers.






61 is positive, and so, 


Certified Tutor
All AP Calculus AB Resources




















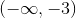
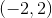
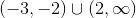


















![y=\sqrt[3]{\frac{3x^4}{4}+C}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1048699/gif.latex)

![y=\pm \sqrt[3]{\frac{3x^4}{4}+C}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1048700/gif.latex)
![y=\sqrt[3]{\frac{x^4}{4}+C}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1048702/gif.latex)



![y=\sqrt[3]{\frac{3x^4}{4}+C}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1048767/gif.latex)























