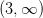All AP Calculus AB Resources
Example Questions
Example Question #26 : Derivative As A Function
Determine the intervals on which the function is decreasing:

To determine the intervals on which the function is decreasing, we must determine the intervals on which the function's first derivative is negative.
The first derivative of the function is equal to
and was found using the following rules:


Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval the first derivative is negative, and on the second interval the first derivative is positive. Thus, the function is decreasing on the first interval, 
Example Question #27 : Derivative As A Function
Determine the relative maxima of the following function:
The function has no relative maxima
To determine the values at which the function has a relative maximum, we must determine the intervals on which the function's first derivative changes from positive to negative.
The first derivative of the function is equal to
and was found using the following rules:

Next, we must find the critical values, at which the first derivative is equal to zero:
Note that we used factoring by grouping to determine the critical values.
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is negative, on the second interval, the first derivative is positive, on the third interval, the first derivative is negative, and on the fourth interval, the first derivative is positive. The first derivative changes from positive to negative at 
Example Question #28 : Derivative As A Function
Determine the intervals on which the function is decreasing:
To determine the intervals on which the function is decreasing, we must determine the intervals on which the function's first derivative is negative.
The first derivative of the function is equal to
and was found using the following rules:
Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is positive, on the second interval, the first derivative is negative, on the third interval, the first derivative is positive, on the fourth interval, the first derivative is negative, and on the fifth interval, the first derivative is positive. So, the function is decreasing on the intervals 
Example Question #29 : Derivative As A Function
Determine the intervals on which the function is decreasing:
None of the other answers
To determine the intervals on which the function is decreasing, we must determine the intervals on which the function's first derivative is negative.
The first derivative of the function is equal to
and was found using the following rules:

Next, we must find the critical values, at which the first derivative is equal to zero:
Note that the square root of a negative number isn't real, so the only critical values come from the first term.
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is positive, on the second interval, the first derivative is negative, and on the third interval, the first derivative is positive. Therefore, the function is decreasing on the second interval, 
Example Question #1 : Applications Of Derivatives
At what point does 
To find out where it shifts from decreasing to increasing, we need to look at the first derivative. The shift will happen where the first derivative goes from a negative value to a positive value.
To find the first derivative for this problem, we can use the power rule. The power rule states that we lower the exponent of each of the variables by one and multiply by that original exponent.
Remember that anything to the zero power is one.
Can this equation be negative? Yes. Does it shift from negative to positive? Yes. Therefore, it will shift from negative to positive at the point that 
Example Question #31 : Derivative As A Function
Determine the intervals on which the function is increasing:
To determine the intervals on which the function is increasing, we must determine the intervals on which the function's first derivative is positive.
The first derivative of the function is equal to
and was found using the following rules:

Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is positive, on the second interval, the first derivative is negative, and on the third interval, the first derivative is positive. The function, therefore, is increasing on the intervals 
Example Question #21 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'
Determine the relative minima of the function:
To determine the values at which the function has a relative minimum, we must determine the intervals on which the function's first derivative changes from negative to positive.
The first derivative of the function is equal to
and was found using the following rule:
Next, we must find the critical values, at which the first derivative is equal to zero:
Note that we stop finding critical values when we have reached the end of the interval of x values.
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is positive, on the second interval, the first derivative is negative, and on the third interval, the first derivative is positive. Thus, a relative minimum occurs at 
Example Question #33 : Derivative As A Function
Determine the intervals on which the function is decreasing:
To determine the intervals on which the function is decreasing, we must determine the intervals on which the function's first derivative is negative.
The first derivative of the function is equal to
and was found using the following rules:
Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is positive, on the second interval, the first derivative is negative, and on the third interval, the first derivative is positive. Thus, the function is decreasing on the interval 
Example Question #34 : Derivative As A Function
Find the intervals on which the following function is increasing:
None of the other answers
To determine the intervals on which the function is increasing, we must determine the intervals on which the function's first derivative is negative.
The first derivative of the function is equal to
and was found using the following rules:


Next, we must find the critical values, at which the first derivative is equal to zero:
Note that the interval stated in the beginning of the problem means the critical values must stay within this interval as well.
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is negative, but on the second interval, the first derivative is positive; the function is therefore increasing on the second interval, 
Example Question #35 : Derivative As A Function
Determine the relative minima of the function:
The function has no relative minima
To determine the values at which the function has relative minima we must determine the intervals on which the function's first derivative changes from negative to positive.
The first derivative of the function is equal to
and was found using the following rules:

Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is negative, and on the second interval, the first derivative is positive. Thus, a relative minimum exists at 
Certified Tutor
All AP Calculus AB Resources