Chain rule and implicit differentiation
Help Questions
AP Calculus AB › Chain rule and implicit differentiation
Find the derivative of the function:
Explanation
On this problem we have to use chain rule, which is:
So in this problem we let
and

Since
and

we can conclude that
Find the derivative of 
Explanation
This is a chain rule derivative. We must first start by taking the derivative of the outermost function. Here, that is a function raised to the fifth power. We need to take that derivative (using the the power rule). Then, we multiply by the derivative of the innermost function:
Find the derivative of the function:
Explanation
*****************************************************************
REQUIRED KNOWLEDGE
*****************************************************************
This problem requires us to understand two things:
-
The derivative of the function
is always
by itself
-
By adding an operation to the variable in the exponent (in our case, the -s instead of just s), we must multiply the derivative by the derivative of the argument in the exponent. This is an application of the chain rule of derivation
*****************************************************************
SOLUTION STEPS
*****************************************************************
Thus:

Thus, the correct answer is:
*****************************************************************
CORRECT ANSWER
*****************************************************************
*****************************************************************
PROBLEMS?
*****************************************************************
If you did not understand the concepts required to solve this derivative problem:
- Look into the derivative of e raised to an argument
- Practice applying the chain rule to derivative problems
Calculate the derivative of 
Explanation
We know how to take the derivative of 

According to the chain rule, we should take the derivative of the outside function and multiply it by the derivative of the inside function. This gives us:
Remember that 
Our final answer:
Given the relation 

None of the other answers
Explanation
We start by taking the derivative of both sides of the equation, and proceeding as follows,

Find 
Explanation
To find 
Taking 
using the following rules:


Note that for every derivative of a function with y, the additional term 

Using algebra to rearrange, we get
Find the derivative of the following function:

Explanation
For a chain rule derivative, we need to work our way inward from the very outermost function. First, we need to do a power rule for the outer exponent. Then, we multiply that by the derivative of the inside.
Given the function 
Explanation
Given the function 
where 




Find
Explanation
We are going to use three rules along with the chain rule:
So then, using our first rule and the chain rule
then using our second rule and chain rule
then using our third rule (no chain rule this time)
Then we rearrange the equation for simplification,

and
Find the derivative of
None of these answers
Explanation
The chain rule of the derivative always deals with the composition of two or more functions.
In this case we can identify two,
and

So 
With chain rule, you always start on the outermost function and work your way inward, which in this case is:
Always the derivative of the outermost evaluated at the inner, multiplied by the derivative of the inner.

















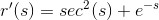


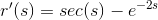
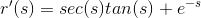


















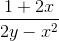


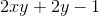













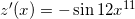
![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/970854/gif.latex)
























