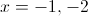All Algebra II Resources
Example Questions
Example Question #311 : Polynomials
Find the values of 
If 

This happens when x = 1 or when x = -2.
Therefore the correct answer is 
Example Question #2 : Properties Of Fractions
Simply the expression:
In order to simplify the expression 
Example Question #3 : Properties Of Fractions
Simplify the expression:
In order to simplify the expression 
Find the Least Common Denominator (LCD) of both terms:
Finally, combine like terms:
Example Question #3 : Understanding Rational Expressions
Simplify the expression:
1. Create a common denominator between the two fractions.
2. Simplify.
Example Question #1671 : Algebra Ii
Find the values of 
For a rational expression to be undefined, the denominator must be equal to 
1. Set the denominator equal to 
2. Set the factors equal to 

and
Example Question #1 : Understanding Rational Expressions
Which value of 
A rational expression is undefined when the denominator is zero.
The denominator is zero when 
Example Question #7 : Properties Of Fractions
Compute:
The terms cannot be added unless the denominators are common. To get the same denominator for each term, find the LCD by multiplying 


The denominator for the three terms are 
Example Question #3 : Properties Of Fractions
Bob is left with a whole pizza for dinner. He eats 

A whole pizza is one unit.
After Bob ate 

Wendy eats an 


Example Question #9 : Properties Of Fractions
Simplify, if possible:
In order to subtract the numerators, first find the least common denominator in the problem. This can usually be found by multiplying the unlike denominators together.
For each term, multiply the numerator with what was multiplied on the denominator to get the least common denominator.
Simplify.
There are no other terms or common factors here that can be simplified. Since there are no like terms in the numerator or denominator, this is fully simplified.
The answer is:
Example Question #11 : Rational Expressions
Simplify:
In order to simplify, we will need a common denominator.
Multiply the denominators together.
This will be the new denominator.
Convert the fractions.
Combine the fractions as a single fraction.
Subtract the numerators.
The answer is:
Certified Tutor
All Algebra II Resources