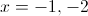All Algebra II Resources
Example Questions
Example Question #1 : How To Find The Solution Of A Rational Equation With A Binomial Denominator
Which of the following fractions is NOT equivalent to 
We know that 


By this property, there is no way to get 

Therefore the correct answer is 
Example Question #1 : Understanding Rational Expressions
Determine the domain of
All real numbers
Because the denominator cannot be zero, the domain is all other numbers except for 1, or
Example Question #2 : Understanding Rational Expressions
Simplify:
This problem is a lot simpler if we factor all the expressions involved before proceeding:
Next let's remember how we divide one fraction by another—by multiplying by the reciprocal:

In this form, we can see that a lot of terms are going to start canceling with each other. All that we're left with is just 
Example Question #1 : Understanding Rational Expressions
Which of the following is the best definition of a rational expression?
The rational expression is a ratio of two polynomials.
The denominator cannot be zero.
An example of a rational expression is:
The answer is:
Example Question #311 : Variables
Find the values of 
If 

This happens when x = 1 or when x = -2.
Therefore the correct answer is 
Example Question #2 : Properties Of Fractions
Simply the expression:
In order to simplify the expression 
Example Question #3 : Properties Of Fractions
Simplify the expression:
In order to simplify the expression 
Find the Least Common Denominator (LCD) of both terms:
Finally, combine like terms:
Example Question #2 : Understanding Rational Expressions
Simplify the expression:
1. Create a common denominator between the two fractions.
2. Simplify.
Example Question #3 : Understanding Rational Expressions
Find the values of 
For a rational expression to be undefined, the denominator must be equal to 
1. Set the denominator equal to 
2. Set the factors equal to 

and
Example Question #4 : Understanding Rational Expressions
Which value of 
A rational expression is undefined when the denominator is zero.
The denominator is zero when 
All Algebra II Resources