Inverse Functions
Help Questions
Algebra 2 › Inverse Functions
Determine the inverse of:
Explanation
Interchange the x and y variables and solve for y.
Add four on both sides.
Simplify both sides.
Divide by seven on both sides.
The answer is:
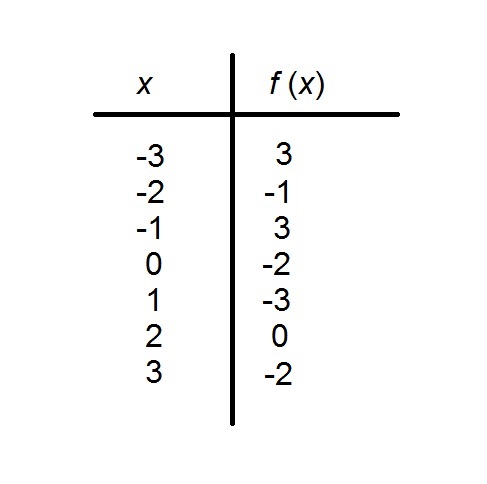
The above table shows a function with domain 
True or false: 
False
True
Explanation
A function 




If we order the rows by range value, we see this to not be the case:



Determine the inverse:
Explanation
In order to find the inverse of this function, interchange the x and y-variables.
Subtract three from both sides.
Simplify the equation.
Divide by ten on both sides.
Simplify both sides.
The answer is:
Determine the inverse of:
Explanation
Interchange the x and y-variables.
Solve for y. Add one-half on both sides.
Simplify both sides.
Multiply five over two on both sides in order to isolate the y-variable.
Apply the distributive property on the left side. The right side will reduce to just a lone y-variable.
The answer is:
Which of the following represents 
Explanation
The question is asking for the inverse function. To find the inverse, first switch input and output -- which is usually easiest if you use 


Here's where we switch:
To solve for 

Distribute:
Get all the 
Factor out a 
Divide by 
This is our inverse function!
Determine the inverse function given the equation:
Explanation
Interchange the x and y variables.
Solve for y. Add six on both sides.
Divide both sides by negative four.
The answer is:
Find the inverse function:
Explanation
Interchange the x and y-variables.
Solve for y. Divide by two on both sides.
Add 
Subtract 
Simplify both sides.
The answer is:
Determine the inverse of:
Explanation
Switch the x and y variables.
Solve for y. Subtract 27 on both sides.
Divide both sides by 9.
The answer is:
Determine the inverse of:
Explanation
Interchange the x and y variables.
Solve for y.
Add 12 on both sides of the equation.
Divide both sides by three.
The answer is:

Define a function 

Which table correctly gives 





Explanation
One definition of the inverse function 







or, ordering the 




























































































