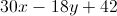All SSAT Middle Level Math Resources
Example Questions
Example Question #1 : Variables
Which of the following is NOT the same as
The answer shows that the 3 in front of the 

Example Question #2 : Variables
Simplify:
Apply the distributive property:
Example Question #3 : Variables
Simplify:
Apply the distributive property:
Example Question #4 : Variables
Simplify:
Apply the distributive property:

Example Question #5 : Variables
Simplify:
Apply the distributive property:
Example Question #6 : How To Multiply Variables
Shaun has twice as much money as Jessica. Jessica has one third as much money as Chris. Shaun has half as much money as Carmen. Who has the most money?
Shaun
Carmen
Chris
Both Shaun and Carmen
Jessica
Carmen
In order to figure out who has the most money, we must organize the data we have. Since Shaun has more money than Jessica, let us use Jessica as our baseline. So, if the money that Jessica has is represented by 

Jessica =
Shaun =
Next, we know that Jessica has one third as much money as Chris. In other words, Chris has three times as much money as Jessica. This can be represented by 



Jessica =
Shaun =
Chris =
Carmen =
Carmen is the answer.
Example Question #7 : How To Multiply Variables
Given 





Example Question #1 : Multiplying And Dividing Polynomials
Simplify:
To solve, you can use the commutative and associative properties of multiplication to group like-terms together.
The 4 and 3 should be first multiplied, resulting in 12.
Next 


12 times 

Therefore, the correct answer is 
Example Question #6 : Variables
Simplify:
When simplifying this expression, the first step is to apply the distributive property.
Next, we assert whether the expression can be reduced further. It cannot, as there are no like-terms to combine.
Therefore, the correct answer is 
Example Question #5 : Variables
Suppose you know the values of all variables in the expression
and you want to evaluate the expression.
In which order will you carry out the operations?
Squaring, multiplying, adding
Adding, multiplying, squaring
Multiplying, adding, squaring
Multiplying, squaring, adding
Adding, squaring, multiplying
Adding, squaring, multiplying
By the order of operations, the operation inside grouping symbols, which here is addition, takes precendence, followed by, in order, squaring and multiplication.
All SSAT Middle Level Math Resources