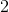How to graph a quadratic function
Help Questions
SAT Math › How to graph a quadratic function
Which of the following functions represents a parabola that has a vertex located at (–3,4), and that passes through the point (–1, –4)?
f(x) = _x_2 – 5
f(x) = –2_x_2 – 12_x_ – 14
f(x) = 2_x_2 + 4_x_ – 2
f(x) = x_2 + 6_x + 13
f(x) = 2_x_2 – 12_x_ – 14
Explanation
Because we are given the vertex of the parabola, the easiest way to solve this problem will involve the use of the formula of a parabola in vertex form. The vertex form of a parabola is given by the following equation:
f(x) = a(x – h)2 + k, where (h, k) is the location of the vertex, and a is a constant.
Since the parabola has its vertex as (–3, 4), its equation in vertex form must be as follows:
f(x) = a(x – (–3)2 + 4 = a(x + 3)2 + 4
In order to complete the equation for the parabola, we must find the value of a. We can use the point (–1, –4), through which the parabola passes, in order to determine the value of a. We can substitute –1 in for x and –4 in for f(x).
f(x) = a(x + 3)2 + 4
–4 = a(–1 + 3)2 + 4
–4 = a(2)2 + 4
–4 = 4_a_ + 4
Subtract 4 from both sides.
–8 = 4_a_
Divide both sides by 4.
a = –2
This means that the final vertex form of the parabola is equal to f(x) = –2(x + 3)2 + 4. However, since the answer choices are given in standard form, not vertex form, we must expand our equation for f(x) and write it in standard form.
f(x) = –2(x + 3)2 + 4
= –2(x + 3)(x + 3) + 4
We can use the FOIL method to evaluate (x + 3)(x + 3).
= –2(x_2 + 3_x + 3_x_ + 9) + 4
= –2(x_2 + 6_x + 9) + 4
= –2_x_2 – 12_x_ – 18 + 4
= –2_x_2 – 12_x_ – 14
The answer is f(x) = –2_x_2 – 12_x_ – 14.
The graph of f(x) is shown above. If f(x) = _ax_2 + bx + c, where a, b, and c are real numbers, then which of the following must be true:
I. a < 0
II. c < 0
III. b_2 – 4_ac < 0
I only
II only
I and II only
I and III only
II and III only
Explanation
Let's examine I, II, and III separately.
Because the parabola points downward, the value of a must be less than zero. Thus, a < 0 must be true.
Next, let's examine whether or not c < 0. The value of c is related to the y-intercept of f(x). If we let x = 0, then f(x) = f(0) = a(0) + b(0) + c = c. Thus, c is the value of the y-intercept of f(x). As we can see from the graph of f(x), the y-intercept is greater than 0. Therefore, c > 0. It is not possible for c < 0. This means choice II is incorrect.
Lastly, we need to examine b_2 – 4_ac, which is known as the discriminant of a quadratic equation. According to the quadratic formula, the roots of a quadratic equation are equal to the following:
Notice, that in order for the values of x to be real, the value of b_2 – 4_ac, which is under the square-root sign, must be greater than or equal to zero. If b_2 – 4_ac is negative, then we are forced to take the square root of a negative number, which produces an imaginary (nonreal) result. Thus, it cannot be true that b_2 – 4_ac < 0, and choice III cannot be correct.
Only choice I is correct.
The answer is I only.
Let f(x) = ax2 + bx + c, where a, b, and c are all nonzero constants. If f(x) has a vertex located below the x-axis and a focus below the vertex, which of the following must be true?
I. a < 0
II. b < 0
III. c < 0
I only
I and III only
II and III only
I and II only
I, II, and III
Explanation
f(x) must be a parabola, since it contains an x2 term. We are told that the vertex is below the x-axis, and that the focus is below the vertex. Because a parabola always opens toward the focus, f(x) must point downward. The general graph of the parabola must have a shape similar to this:
Since the parabola points downward, the value of a must be less than zero. Also, since the parabola points downward, it must intersect the y-axis at a point below the origin; therefore, we know that the value of the y-coordinate of the y-intercept is less than zero. To find the y-coordinate of the y-intercept of f(x), we must find the value of f(x) where x = 0. (Any graph intersects the y-axis when x = 0.) When x = 0, f(0) = a(0) + b(0) + c = c. In other words, c represents the value of the y-intercept of f(x), which we have already established must be less than zero. To summarize, a and c must both be less than zero.
The last number we must analyze is b. One way to determine whether b must be negative is to assume that b is NOT negative, and see if f(x) still has a vertex below the x-axis and a focus below the vertex. In other words, let's pretend that b = 1 (we are told b is not zero), and see what happens. Because we know that a and c are negative, let's assume that a and c are both –1.
If b = 1, and if a and c = –1, then f(x) = –x2 + x – 1.
Let's graph f(x) by trying different values of x.
If x = 0, f(x) = –1.
If x = 1, f(x) = –1.
Because parabolas are symmetric, the vertex must have an x-value located halfway between 0 and 1. Thus, the x-value of the vertex is 1/2. To find the y-value of the vertex, we evaluate f(1/2).
f(1/2) = –(1/2)2 + (1/2) – 1 = –1/4 + (1/2) – 1 = –3/4.
Thus, the vertex of f(x) would be located at (1/2, –3/4), which is below the x-axis. Also, because f(0) and f(1) are below the vertex, we know that the parabola opens downward, and the focus must be below the vertex.
To summarize, we have just provided an example in which b is greater than zero, where f(x) has a vertex below the x-axis and a focus below the vertex. In other words, it is possible for b > 0, so it is not true that b must be less than 0.
Let's go back to the original question. We know that a and c are both less than zero, so we know choices I and III must be true; however, we have just shown that b doesn't necessarily have to be less than zero. In other words, only I and III (but not II) must be true.
The answer is I and III only.
A farmer is designing rectangular pen for his cows. One side of the pen will be blocked by a steep hill, and the other three sides of the pen will be fenced off with wire. If the farmer has 20 meters of wire, what is the maximum area of the pen that he can build in square meters?
75
75/2
25
25/2
50
Explanation
Let l = length and w = width of the pen. Let us assume that the side blocked by the mountain is along the length of the pen.
The length of wire used to make the pen must equal l + 2w, because this is the perimeter of a rectangle, excluding one of the lengths. The area of the pen will equal l x w.
l + 2w = 20
l = 20-2w
A = l x w = (20-2w)(w) = 20w - 4w2
Let A be a function of w, such that A(w) = 20w - 4w2. We want to find the maximum value of A. We recognize that the graph of A must be in the shape of a parabola, pointing downward. The maximum value of the parabola will thus occur at the vertex.
We want to rewrite A(w) in the standard form of a parabola, given by f(x) = a(x-h)2+k. In order to do this, we must complete the square.
20w-4w2 = -4w2+20w = -4(w2-5w) = -4(w2-5w + 25/4) + 25 = -4(w-5/2)2+25
Thus, the vertex of the parabola occurs at (5/2, 25), which means that w = 5/2.
Going back to our original equation, l + 2(5/2) = 20, and l = 15.
A = l x w = 15(5/2) = 75/2

What is the equation of the graph?
Explanation
In order to figure out what the equation of the image is, we need to find the vertex. From the graph we can determine that the vertex is at 
Recall vertex form,





Plugging in our values, we get
To solve for 
I will pick 
Now our equation is
Let's expand this,
Let f(x) = x2. By how many units must f(x) be shifted downward so that the distance between its x-intercepts becomes 8?
2
4
8
12
16
Explanation
Because the graph of f(x) = x2 is symmetric about the y-axis, when we shift it downward, the points where it intersects the x-axis will be the same distance from the origin. In other words, we could say that one intercept will be (-a,0) and the other would be (a,0). The distance between these two points has to be 8, so that means that 2a = 8, and a = 4. This means that when f(x) is shifted downward, its new roots will be at (-4,0) and (4,0).
Let g(x) be the graph after f(x) has been shifted downward. We know that g(x) must have the roots (-4,0) and (4,0). We could thus write the equation of g(x) as (x-(-4))(x-4) = (x+4)(x-4) = x2 - 16.
We can now compare f(x) and g(x), and we see that g(x) could be obtained if f(x) were shifted down by 16 units; therefore, the answer is 16.
Which of the following is true about the quadratic function f(x)=(x+4)2 - 3?
The graph is a parabola whose vertex is (4,-3).
The function is one-to-one.
The function is even.
The graph is a parabola with two x-intercepts.
The graph is a parabola with two y-intercepts.
Explanation
The function is given in vertex form, which is (x-h)2+k where the vertex of the parabola is the point (h,k). In this particular function, h=-4 and k=3, so the vertex is (-4,-3). No parabola is one-to-one, as they don't pass the horizontal line test. While parabolas can be even functions, this will only happen when the vertex is on the y-axis (or when h=0) because even functions must be symmetric with respect to the y-axis. No function can have two y-intercepts, as it would then not pass the vertical line test and not be a function. This parabola does have two x-intercepts, however. This can be shown by setting y=0 and solving for x, or by simply realizing that the vertex is below the x-axis and the parabola opens up.
The parabolas of the functions 

If we define 


None of the other responses gives a correct answer.
Explanation
The eqiatopm of 

so the vertex of its parabola is 




For the function 



Of the five choices, the only equation of 


To verify, graph both functions on the same grid.

How many times does the equation below cross the x-axis?
Explanation
You can solve this problem two ways.
3. You can solve for where the graph crosses the x-axis by setting the equation equal to zero, factoring, and solving.
2. You can quickly sketch the graph by choosing some x values and solving for y.


We see that the graph passes the x-axis twice.