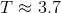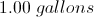All SAT II Math I Resources
Example Questions
Example Question #1 : Other Mathematical Relationships
Multiply in modulo 6:
In modulo 6 arithmetic, a number is congruent to the reainder of its division by 6.
Therefore, since 


The correct response is 0.
Example Question #2 : Other Mathematical Relationships
Which is an example of a set that is not closed under addition?
The set of all integers between 1 and 10 inclusive
All of the sets given in the other responses are closed under addition.
The set of all negative integers
The set
The set of all positive even integers
The set of all integers between 1 and 10 inclusive
A set is closed under addition if and only if the sum of any two (not necessarily distinct) elements of the set is also an element of the set.

The set of all negative integers is closed under addition, since any two negative integers can be added to yield a third negative integer.
The set of all positive even integers is closed under addition, since any two positive even integers can be added to yield a third positive even integer.
The remaining set is the set of all integers between 1 and 10 inclusive. It is not closed under addition, as can be seen by this counterexample:
but
Example Question #3 : Other Mathematical Relationships


If 






We can write this relationship alternatively as
where the initial conditions can be substituted on the left side and final conditions, on the right. We will be solving for 
Example Question #71 : Mathematical Relationships



If 








We can write this relationship alternatively as
where the initial conditions can be substituted on the left side and final conditions, on the right. We will be solving for 
Example Question #1 : Proportionalities
Sarah notices her map has a scale of 


So to find out the distance between the cities
Example Question #73 : Mathematical Relationships
If an object is hung on a spring, the elongation of the spring varies directly as the mass of the object. A 20 kg object increases the length of a spring by exactly 7.2 cm. To the nearest tenth of a centimeter, by how much does a 32 kg object increase the length of the same spring?
Let 

We can find 

so
In the second situation, we set 


which rounds to 11.5 centimeters.
Example Question #1 : Understanding Direct Proportionality
Sunshine paint is made by mixing three parts yellow paint and one part red paint. How many gallons of yellow paint should be mixed with two quarts of red paint?
(1 gallon = 4 quarts)
First set up the proportion:
x =
Then convert this to gallons:
Example Question #1 : Direct Proportionality
Sally currently has 192 books. Three months ago, she had 160 books. By what percentage did her book collection increase over the past three months?
To find the percentage increase, divide the number of new books by the original amount of books:
She has 32 additional new books; she originally had 160.
Example Question #3 : Basic Single Variable Algebra
Find 

To find x we need to find the direct proportion. In order to do this we need to cross multiply and divide.
From here we mulitply 100 and 1 together. This gets us 100 and now we divide 100 by 4 which results in
Example Question #77 : Mathematical Relationships
On a map of the United States, Mark notices a scale of 










If the real distance between the two cities is 







All SAT II Math I Resources