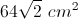Squares
Help Questions
PSAT Math › Squares
Square X has 3 times the area of Square Y. If the perimeter of Square Y is 24 ft, what is the area of Square X, in sq ft?
54
72
112
144
108
Explanation
Find the area of Square Y, then calculate the area of Square X.
If the perimeter of Square Y is 24, then each side is 24/4, or 6.
A = 6 * 6 = 36 sq ft, for Square Y
If Square X has 3 times the area, then 3 * 36 = 108 sq ft.
Square X has 3 times the area of Square Y. If the perimeter of Square Y is 24 ft, what is the area of Square X, in sq ft?
54
72
112
144
108
Explanation
Find the area of Square Y, then calculate the area of Square X.
If the perimeter of Square Y is 24, then each side is 24/4, or 6.
A = 6 * 6 = 36 sq ft, for Square Y
If Square X has 3 times the area, then 3 * 36 = 108 sq ft.
ABCD and EFGH are squares such that the perimeter of ABCD is 3 times that of EFGH. If the area of EFGH is 25, what is the area of ABCD?
5
15
25
75
225
Explanation
Assign variables such that
One side of ABCD = a
and One side of EFGH = e
Note that all sides are the same in a square. Since the perimeter is the sum of all sides, according to the question:
4a = 3 x 4e = 12e or a = 3e
From that area of EFGH is 25,
e x e = 25 so e = 5
Substitute a = 3e so a = 15
We aren’t done. Since we were asked for the area of ABCD, this is a x a = 225.
ABCD and EFGH are squares such that the perimeter of ABCD is 3 times that of EFGH. If the area of EFGH is 25, what is the area of ABCD?
5
15
25
75
225
Explanation
Assign variables such that
One side of ABCD = a
and One side of EFGH = e
Note that all sides are the same in a square. Since the perimeter is the sum of all sides, according to the question:
4a = 3 x 4e = 12e or a = 3e
From that area of EFGH is 25,
e x e = 25 so e = 5
Substitute a = 3e so a = 15
We aren’t done. Since we were asked for the area of ABCD, this is a x a = 225.
If the perimeter of a square is equal to twice its area, what is the length of one of its sides?
Explanation
Area of a square in terms of each of its sides:
Area = S x S
Perimeter of a square:
Perimeter = 4S
So if 'the perimeter of a square is equal to twice its area':
2 x Area = Perimeter
2 x \[S x S\] = \[4S\]; divide by 2:
S x S = 2S; divide by S:
S = 2
If the perimeter of a square is equal to twice its area, what is the length of one of its sides?
Explanation
Area of a square in terms of each of its sides:
Area = S x S
Perimeter of a square:
Perimeter = 4S
So if 'the perimeter of a square is equal to twice its area':
2 x Area = Perimeter
2 x \[S x S\] = \[4S\]; divide by 2:
S x S = 2S; divide by S:
S = 2
When the side of a certain square is increased by 2 inches, the area of the resulting square is 64 sq. inches greater than the original square. What is the length of the side of the original square, in inches?
14
15
16
17
18
Explanation
Let x represent the length of the original square in inches. Thus the area of the original square is x2. Two inches are added to x, which is represented by x+2. The area of the resulting square is (x+2)2. We are given that the new square is 64 sq. inches greater than the original. Therefore we can write the algebraic expression:
x2 + 64 = (x+2)2
FOIL the right side of the equation.
x2 + 64 = x2 + 4x + 4
Subtract x2 from both sides and then continue with the alegbra.
64 = 4x + 4
64 = 4(x + 1)
16 = x + 1
15 = x
Therefore, the length of the original square is 15 inches.
If you plug in the answer choices, you would need to add 2 inches to the value of the answer choice and then take the difference of two squares. The choice with 15 would be correct because 172 -152 = 64.
When the side of a certain square is increased by 2 inches, the area of the resulting square is 64 sq. inches greater than the original square. What is the length of the side of the original square, in inches?
14
15
16
17
18
Explanation
Let x represent the length of the original square in inches. Thus the area of the original square is x2. Two inches are added to x, which is represented by x+2. The area of the resulting square is (x+2)2. We are given that the new square is 64 sq. inches greater than the original. Therefore we can write the algebraic expression:
x2 + 64 = (x+2)2
FOIL the right side of the equation.
x2 + 64 = x2 + 4x + 4
Subtract x2 from both sides and then continue with the alegbra.
64 = 4x + 4
64 = 4(x + 1)
16 = x + 1
15 = x
Therefore, the length of the original square is 15 inches.
If you plug in the answer choices, you would need to add 2 inches to the value of the answer choice and then take the difference of two squares. The choice with 15 would be correct because 172 -152 = 64.
If the area of a square is 25 inches squared, what is the perimeter?
20
25
10
15
Not enough information
Explanation
The area of a square is equal to length times width or length squared (since length and width are equal on a square). Therefore, the length of one side is 

If the diagonal of a square measures 
Explanation
This is an isosceles right triangle, so the diagonal must equal