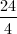All ISEE Middle Level Quantitative Resources
Example Questions
Example Question #661 : Isee Middle Level (Grades 7 8) Quantitative Reasoning
Which is the greater quantity?
(a) The reciprocal of
(b) The reciprocal of
(b) is greater
(a) and (b) are equal
(a) is greater
It is impossible to tell from the information given
(b) is greater
The reciprocal of any fraction can be found by switching numerator and denominator. Since both numbers are negative, both reciprocals will be negative.
(a) 
(b) 
We can compare these by writing them both with common denominator 
making (b) greater
Example Question #661 : Isee Middle Level (Grades 7 8) Quantitative Reasoning
Which is the greater quantity?
(a) The reciprocal of
(b) The reciprocal of
(b) is greater
(a) and (b) are equal
It cannot be determined from the information given
(a) is greater
(b) is greater
The reciprocal of any fraction can be found by switching numerator and denominator.
(a) 
(b) 
We can compare these by writing them both with common denominator 
making (b) greater
Example Question #1 : Fractions
When dealing with math problems that involve fractions and whole numbers or mixed numbers, you should first convert the non-fraction into a fraction:
The problem should look like this:
When dividing with fractions, you need to find the reciprocal of the second fraction before you can do anything else. In other words, flip the second number.
When you find the reciprocal of the second number, change the problem from division to multiplication. The new problem should look like this:

The answer is 6.
Example Question #1 : How To Divide Fractions
When dividing fractions, you must first find the reciprocal of the second number in the operation. In other words, flip the second fraction.
When you do this, the operation also changes from division to multiplication. The problem should now look like this:
Then multiply both the numerators and denominators.
When possible, always reduce the fraction. In this case, both 2 and 8 are divisible by 2.
The result is your answer.
Example Question #1 : Numbers And Operations
When dividing fractions, you must first find the reciprocal of the second fraction. In other words, flip the second fraction.
When you do this, the operation also changes from division to multiplication. The problem should now look like this:
Multiply the numerators and denominators. The result is your answer.
Example Question #1 : Numbers And Operations
When dealing with fractions and whole numbers, first convert the whole number to a fraction. This is easily done by putting the whole number over 1.
When dividing fractions, you must first find the reciprocal of the second fraction in the operation. In other words, flip the second fraction.
When you do this, the operation changes from division to multiplication. The problem should now look like this:
Solve the multiplication by multiplying the numerators and the denominators.
Since the result is 
Example Question #662 : Isee Middle Level (Grades 7 8) Quantitative Reasoning
If Candy has 
Candy has 

To find the reciprical of a fraction, we switch the numerator and denominator.


Now we multiply 

Each person gets 
Example Question #2 : Numbers And Operations

Which is the greater quantity?
(a)
(b)
(a) is the greater quantity
(a) and (b) are equal
(b) is the greater quantity
It is impossible to determine which is greater from the information given
(a) is the greater quantity
Division by a fraction is equivalent to multiplication by its reciprocal, so



or

Example Question #9 : Fractions




If 

The reciprocal of 

Example Question #10 : Fractions
The reciprocal of 

(a) The reciprocal of
(b)
(a) is the greater quantity
It is impossible to determine which is greater from the information given
(b) is the greater quantity
(a) and (b) are equal
(b) is the greater quantity
The reciprocal of 


The reciprocal of 

Certified Tutor
Certified Tutor
All ISEE Middle Level Quantitative Resources