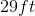To find the area of the figure above, we need to slip the figure into two rectangles.

Using our area formula, , we can solve for the area of both of our rectangles

To find our final answer, we need to add the areas together.

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.

First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:

Substitute in our side lengths.

Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by .

Thus, the area formula for a right triangle is as follows:

or

Add up all of the sides of a triangle to get the perimeter. Here, 2 of the sides add up to give you 9 inches. The third side must equal the difference between 14 inches and 9 inches.

To find the area of a triangle, we will use the following formula:

where b is the base and h is the height of the triangle.

So, we know the base is 6cm and the height is 7cm. Knowing this, we can substitute into the formula. We get

Add up all of the sides of a triangle to get the perimeter. Here, 2 of the sides add up to give you 9 inches. The third side must equal the difference between 14 inches and 9 inches.

The fence is going around the garden, so this is a perimeter problem.

When we are given coordinate points, it's important to know the difference between the x-axis and the y-axis, and which order these points are given. The x-axis is the axis that runs left to right and the y-axis is the axis the runs up and down. When coordinate points are written, the x value goes first, followed by the y value .

Knowing this information, we can plot the points and use straight lines to connect them in a counter-clockwise or clockwise direction. The provided coordinate points should create the following graph:

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.

First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:

Substitute in our side lengths.

Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by .

Thus, the area formula for a right triangle is as follows:

or

To find the area of the figure above, we need to slip the figure into two rectangles.

Using our area formula, , we can solve for the area of both of our rectangles

To find our final answer, we need to add the areas together.

This problem asks us to calculate the amount of space that the wallpaper will cover. The amount of space that something covers can be described as its area. In this case area is calculated by using the formula