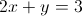All Intermediate Geometry Resources
Example Questions
Example Question #1 : Perpendicular Lines
What line is perpendicular to 




If the lines are perpendicular, then 
Next we substitute the new slope and the given point into the slope-intercept form of the equation to calculate the intercept. So the equation to solve becomes 
So the equation of the perpendicular line becomes 
Example Question #51 : Lines
Which line below is perpendicular to 
The definition of a perpendicular line is one that has a negative, reciprocal slope to another.
For this particular problem, we must first manipulate our initial equation into a more easily recognizable and useful form: slope-intercept form or 
According to our 




Our answer will have a slope of 




(As an aside, the negative reciprocal of 4 is 
Example Question #1 : How To Find The Equation Of A Perpendicular Line
Find the equation of the line perpendicular to 
The definition of a perpendicular line is a line with a negative reciprocal slope and identical intercept.
Therefore we need a line with slope 3 and intercept 2.
This means the only fitting line is 
Example Question #1 : How To Find The Equation Of A Perpendicular Line
Which one of these equations is perpendicular to:
To find the perpendicular line to
we need to find the negative reciprocal of the slope of the above equation.
So the slope of the above equation is 



The negative reciprocal is:
So we are looking for an equation with a 
Only 
Example Question #2 : How To Find The Equation Of A Perpendicular Line
Suppose a line is represented by a function 

Determine the slope of the function 
The slope of a perpendicular line is the negative reciprocal of the original slope. Determine the value of the slope perpendicular to the original function.

Plug in the given point and the slope to the slope-intercept form to find the y-intercept.
Substitute the slope of the perpendicular line and the new y-intercept back in the slope-intercept equation, 
The correct answer is:
Example Question #151 : Coordinate Geometry
Suppose a perpendicular line passes through 

Find the slope from the given equation 

The slope of the perpendicular line is the negative reciprocal of the original slope.
Plug in the perpendicular slope and the given point to the slope-intercept equation.
Plug in the perpendicular slope and the y-intercept into the slope-intercept equation to get the equation of the perpendicular line.
Example Question #3 : Perpendicular Lines
Find a line perpendicular 

Since we need a line perpendicular to 


Example Question #7 : Perpendicular Lines
A line is perpendicular to the line of the equation
and passes through the point 
Give the equation of the line.
A line perpendicular to another line will have as its slope the opposite of the reciprocal of the slope of the latter. Therefore, it is necessary to find the slope of the line of the equation
Rewrite the equation in slope-intercept form 


Add 
Multiply both sides by 
The slope of this line is 


To find 


Add 
The equation, in slope-intercept form, is 
To rewrite in standard form with integer coefficients:
Multiply both sides by 5:
Add 
or
All Intermediate Geometry Resources