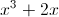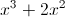Simplifying Exponents
Help Questions
Math › Simplifying Exponents
Order the following from least to greatest:
Explanation
In order to solve this problem, each of the answer choices needs to be simplified.
Instead of simplifying completely, make all terms into a form such that they have 100 as the exponent. Then they can be easily compared.




Thus, ordering from least to greatest: 
Order the following from least to greatest:
Explanation
In order to solve this problem, each of the answer choices needs to be simplified.
Instead of simplifying completely, make all terms into a form such that they have 100 as the exponent. Then they can be easily compared.




Thus, ordering from least to greatest: 
Simplify the following expression.
Explanation
Recall that when we are dividing exponents with the same base, we keep the base the same and subtract the exponents.
Thus, we have 
We also recall that for negative exponents,

Thus, 
Simplify the following expression.
Explanation
Recall that when we are dividing exponents with the same base, we keep the base the same and subtract the exponents.
Thus, we have 
We also recall that for negative exponents,

Thus, 
Simplify the expression:
Explanation
First simplify the second term, and then combine the two:
Simplify the expression:
Explanation
First simplify the second term, and then combine the two:
Simplify the following exponent expression:
Explanation
Begin by rearranging the terms in the numerator and denominator so that the exponents are positive:
Multiply the exponents:
Simplify:
Simplify the following exponent expression:
Explanation
Begin by rearranging the terms in the numerator and denominator so that the exponents are positive:
Multiply the exponents:
Simplify:
What is the largest positive integer, 


16
8
10
5
20
Explanation


What is the largest positive integer, 


16
8
10
5
20
Explanation