All GRE Math Resources
Example Questions
Example Question #1 : How To Find Median
The medians of the following two sets of numbers are equal, and
the sets are arranged in ascending order
{1, 4, x, 8} and {2, 5, y, 9}. What is y – x?
0
3
2
–2
–1
–1
Answer: –1
Explanation: Recall that the median of an even-numbered set of numbers is the arithmetic mean of the pair of middle terms. Thus (4 + x)/2 = median of the first set and (5 + y)/2 = median of the second set. Since both medians are equal, we can set the equations equal to eachother. (4 + x)/2 = (5 + y)/2. Multiply both sides by 2 and we get 4 + x = 5 + y. We also know that 4 < x < 8 and 5 < y < 9, since the sets are arranged in ascending order. This narrows our options for x and y down significantly. Plugging in various values will eventually get you to x = 7 and y = 6, since 7 + 4 = 11 and 5 + 6 = 11, and thus the median in both cases would be 5.5. Thus, y – x = –1.
Example Question #1 : Statistics
What is the median in the following set of numbers?
16, 19, 16, 7, 2, 20, 9, 5
16, 19, 16, 7, 2, 20, 9, 5
Order the numbers from smallest to largest.
2,5,7,9,16,16,19,20
The median is the number in the middle.
In this case, there is a 9 and 16 in the middle.
When that happens, take the average of the two numbers.
Example Question #2 : How To Find Median
Find the median:
To find the median, arrange the numbers from smallest to largest:
4,4,4,4,6,7,9,9,12,12,12,12,12,12,18,76,90
There are 17 numbers in total. Since 17 is an odd number, the median will be the middle number of the set. In this case, it is the 9th number, which is 12.
Example Question #3 : How To Find Median
There are 3,500 people in group A and 5,000 people in group B:
|
Car Type |
% in Group A Who Own |
% in Group B Who Own |
|
Motorbike |
4 |
9 |
|
Sedan |
35 |
25 |
|
Minivan |
22 |
15 |
|
Van |
9 |
12 |
|
Coupe |
3 |
6 |
What is the median of the number of people in group B who own either a minivan, van, or coupe?
Treat the percentages as a list, as we are including every demographic from the 3 vehicle types mentioned. If we do each 0.06(5000), 0.12(5000), and 0.15(5000) we note from observation that the median, or middle value, would have to be the 12% row since the sample size does not change. The question asks for EITHER of the 3 categories, so we can ignore the other two.
0.12(5000) = 600 (van) is the median of the 3 categories.
Example Question #4 : How To Find Median
In the set above, which is larger: the median, the mean, or the mode?
Both median and mean
All are equal
Median
Mode
Mean
Mean
Begin by ordering the set from smallest to largest:
Already, we see that the mode is 8. Find the median by taking the average of the two middle numbers:
Find the mean by adding all numbers and dividing by the total number of terms:
Of the three, the mean of the set is the largest.
Example Question #6 : How To Find Median
The grades on a test taken by 

To solve this problem, we must be aware of the definition of a median for a set of numbers. The median is defined as the number that is in middle of a set of numbers sorted from smallest to largest. Therefore we must first sort the numbers from largest to smallest.
34,43,45,50,56,65,70,76,76,82,87,88,92,95,100
43,45,50,56,65,70,76,76,81,87,88,82,95
45,50,56,65,70,76,76,81,87,88,82
50,56,65,70,76,76,81,87,88
56,65,70,76,76,81,87
65,70,76,76,81
70,76,76
76
Then by slowly eliminating the smallest and the largest numbers we find that the median score for this test is 76.
Example Question #2 : Statistics
Quantity A: The mean of
Quantity B: The median of
The two quantities are equal.
Quantity A is greater.
Quantity B is greater.
The relationship cannot be determined.
Quantity B is greater.
Begin by reordering the set in numerical order:
Then becomes
Since there is an odd number of values, the median is the middle value.
Quantity B:
Now, to find the arithmetic mean, take the sum of values divided by the total number of values.
Quantity A:
Example Question #5 : How To Find Median
The arithmetic mean of 



Now, 
Since there are even number of values, the median is the mean of the two middle most values:
All GRE Math Resources







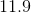


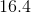















![Set_A=[-10,4,2,-14,-2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/488996/gif.latex)


![Set_A=[-10,4,2,-14,-2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/488997/gif.latex)
![Set_A=[-14,-10,-2,2,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/488998/gif.latex)























