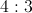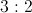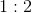All GRE Math Resources
Example Questions
Example Question #1 : How To Find A Ratio
1 : 1
2 : 3
3 : 4
1 : 3
There are 28 students in a room. The ratio of boys to girls cannot be which of the above.
3 : 4
1 : 1
1 : 3
2 : 3
2 : 3
When selecting ratios for two variables (boys and girls) the two sides of the ratio must add up to be a factor of the total student count. The factors of 28 include 14, 7, 4, and 2. (1 + 1 = 2), (2 + 3 = 5), (3 + 4 = 7), and (1 + 3 = 4). 5 is the only nonfactor and cannot be the ratio of boys to girls, thus making 2 : 3 the correct answer.
Example Question #1 : How To Find A Ratio
For All Sweets Bakery, the daily sales ratio of bread to cakes is 5:2. If the bakery sells 12 more loaves of bread on Tuesday than its daily sale of 40 loaves, how many cakes were sold on Tuesday? (round to the nearest integer)
Since 40 loaves of bread are sold daily, and the ratio of bread to cakes is 5:2, then 
Using the ratio in the same way, we can find the additional amount of cakes sold:

Thus, the total amount of cakes sold on Tuesday is 
Example Question #2 : How To Find A Ratio
You are making a cake that requires, by volume, three times as much flour as sugar, twice as much sugar as milk, eight times more milk than baking powder and twice as much baking powder as salt. If you start with a teaspoon of salt, how many cups of flour do you need (there are 48 teaspoons in one cup)?
One teaspoon of salt requires 2 teaspoons of baking powder, which requires 16 teaspoons of milk and 32 teaspoons of sugar. 32 teaspoons of sugar requires 96 teaspoons of flour, which equals two cups of flour.
Example Question #2 : How To Find A Ratio
A bakery stocks 3 cookies for every 2 cupcakes and 6 pastries for every 5 cookies. What is the ratio of cupcakes to pastries?
First, you have to set up the given ratios, which is 3 cookies : 2 cupcakes and 5 cookies : 6 pastries. Then, you find a common multiple of cookies (i.e. 15) and convert the ratios to 15 cookies : 10 cupcakes and 15 cookies : 18 pastries. Since both ratios now have 15 cookies, you can infer that the ration of cupcakes to pastries is 10:18 or 5:9.
Example Question #2 : How To Find A Ratio
The ratio of male students to female students in a class is 13 to 19. If there are 224 people in the class, including one teacher, one administrator, and thirty evaluators, how many people in the class are male students?
91
80
78
133
114
78
Begin by eliminating people in the class who are not students. Subtracting 1 teacher, 1 administrator and 30 evaluators leaves 192 students.
We also need to determine the ratio of male students to total students from the information in the question. Out of every thirty-two students, thirteen are male.
Now we can set up a proportion, and solve for the number of male students.
Example Question #4 : How To Find A Ratio
If the length of a rectangle is increased by 50% and its width is decreased by 20%, what is the ratio of the area of the new rectangle to the original rectangle?
First, pick a number for the original length and width. To make it easy, you can choose a length of 1 and width of 1, which would give it an area of 1. If we increased the length by 50% and decreased the width by 20%, then the dimensions of the new rectangle would be 
Example Question #3 : How To Find A Ratio
There are 3,500 people in group A and 5,000 people in group B:
|
Car Type |
% in Group A Who Own |
% in Group B Who Own |
|
Motorbike |
4 |
9 |
|
Sedan |
35 |
25 |
|
Minivan |
22 |
15 |
|
Van |
9 |
12 |
|
Coupe |
3 |
6 |
What is the ratio of the number of people in group A with motorbikes and vans to the total number of people across both groups with motorbikes and vans?
First find the total number that own both motorbikes and vans of each group separately:
Group A:
Group B:
Now we have a ratio that should be:
Example Question #4 : How To Find A Ratio
A dessert is made using 2 parts cake and 3 parts icing. The cake contains 4 parts sugar, 5 parts milk, and 11 parts of other ingredients. The icing contains 3 parts sugar, 2 parts milk, and 15 parts of other ingredients. Which quantity is greater?
Quantity A: Parts sugar in the dessert
Quantity B: Parts milk in the dessert
Quantity A is greater.
The two quantities are equal.
Quantity B is greater.
The relationship cannot be determined from the information given.
Quantity A is greater.
Quantity A: To determine the parts of sugar in the dessert, we use the following process. Let's first figure out the amount of sugar in the cake. This is 4/20. Next, find the amount of sugar in the icing topping: 3/20. Then, we need to account for the amount of cake and icing in the dessert. Using the fact that there are 2 parts cake and 3 parts icing, we can say that 2/5 of the dessert is cake and 3/5 is icing. Combining this information with the amount of sugar in both the cake and the icing, we obtain: 2/5 * 4/20 + 3/5 * 3/20 = 17/100. So, there are 17 parts of sugar in the dessert.
Quantity B: Use the same method to find the amount of milk: 2/5 * 5/20 + 3/5 * 2/20 = 16/100. So there are 16 parts milk in the dessert. Thus, Quantity A is larger.
Example Question #1 : How To Find A Ratio
The ratio of the number of financial employees who remained in the same role for 2 to 9 years to the number of construction employees who remained in the same role for 0 to 4 years is closest to which of the following?
For this problem, we need to find the number of employees who fall into the categories described, keeping in mind that multiple portions of the pie chart must be accommodated for. Then, we can fit them into a ratio:
For the "2 to 9 years" portion of the financial industry, include
(0.2 + 0.18)(12,000,000) = 4,560,000 workers.
For the "0 to 4 years" portion of the construction industry, include
(0.15 + 0.2)(8,000,000) = 2,800,000 workers.
Now divide and simplify to find the ratio:
4,560,000/2,800,000 = 8/5.
Example Question #1 : How To Find A Ratio
The ratio of 







What is the ratio of 

Since the ratios are fixed, regardless of the actual values of 



In order to convert to a form where we can relate 







Thus, we now have 

Setting the 

All GRE Math Resources