Angles and Quadrilaterals
Help Questions
GED Math › Angles and Quadrilaterals
If the rectangle has a width of 5 and a length of 10, what is the area of the rectangle?
Explanation
Write the area for a rectangle.
Substitute the given dimensions.
The answer is:
In the figure below, find the measure of the largest angle.

Explanation
Recall that in a quadrilateral, the interior angles must add up to 
Thus, we can solve for 
Now, to find the largest angle, plug in the value of 
The largest angle is 
Given Quadrilateral 
I) 
II) 
III) 



Statement II only
Statement III only
Statement I only
Statement I, II, or III
Explanation
Statement I asserts that two pairs of consecutive angles are congruent. This does not prove that the figure is a parallelogram. For example, an isosceles trapezoid has two pairs of congruent base angles, which are consecutive.
Statement II asserts that both pairs of opposite angles are congruent. By a theorem of geometry, this proves the quadrilateral to be a parallelogram.
Statement III asserts that two pairs of consecutive angles are supplementary. While all parallelograms have this characteristic, trapezoids do as well, so this does not prove the figure a parallelogram.
The correct response is Statement II only.
In Rhombus 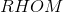







Explanation
The figure referenced is below.

The sides of a rhombus are congruent by definition, so 

Also, consecutive angles of a rhombus are supplementary, as they are with all parallelograms, so





The correct response is that 
You are given Parallelogram 


I)
II)
III)
Statement I, II, or III
Statement III only
Statement II only
Statement I only
Explanation
A rectangle is defined as a parallelogram with four right, or 
Since opposite angles of a paralellogram are congruent, if one angle measures 



In short, in a parallelogram, if one angle is right, all are right and the parallelogram is a rectangle. All three statements assert that one angle is right, so from any one, it follows that the figure is a rectangle. The correct response is Statements I, II, or III.
Note that the sidelengths are irrelevant.
























