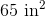Solve for area of a triangle
Help Questions
7th Grade Math › Solve for area of a triangle

What is the area of the triangle pictured above?
12
24
30
40
60
Explanation
The area of a triangle is calculated using the formula 


In triangle ABC above, the distance between point A and point D is 10 inches, and the area of the triangle is 20 square inches. What is the length of side BC?
4 inches
2 inches
10 inches
8 inches
There is not enough information to answer the question
Explanation
The area of a triangle can be calculated using the formula Area = 1/2 * Base * Height. Here you're given two of the unknowns in that formula:
Area = 20
Height = 10
So you can plug those into the area formula to solve for Base, the only remaining unknown:
20 = 1/2 * Base * 10
That means that 20 = 5 * Base, so Base = 4.

In triangle ABC, side BC measures 12 meters, and the shortest straight-line distance between point A and side BC is 5 meters long. What is the area of triangle ABC?
24
60
36
30
12
Explanation
The area of a triangle can be calculated using the formula 

The pictured right triangle has sides of 7, 24, and 25. What is the area of that triangle?
84
77
64
128
125
Explanation
The area of a triangle can be calculated using the formula 
Calculate the area of the provided figure.

Explanation
In order to solve this problem, we need to recall the area formula for a triangle:
Now that we have the correct formula, we can substitute in our known values and solve: