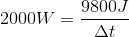All AP Physics 1 Resources
Example Questions
Example Question #1 : Power
A man with mass 50kg is wearing a backpack of mass 5kg and running up a hill with a slope of 30 degrees at a constant velocity of 
Since the man's kinetic energy remains constant, we are really solving for the rate at which he gains potential energy.
However, when we find the change of this with respect to time (aka power), the expression becomes:
We can calculate the change in height by using the velocity of the man and the slope of the hill:
Substituting this into the equation for power, we get:
We know all of these values, so we can plug in and solve:
Example Question #202 : Work, Energy, And Power
An elevator of mass 1000kg has five passengers, each with an average mass of 80kg. The elevator accelerates from rest to a velocity of 
We can use the work-energy theorem to solve this problem, which says the the net work done is equal to the change in kinetic energy:
We can expand this to write:
We know that the elevator was initially at a standstill, so the equation becomes:
We are given the mass of the elevator plus passengers, as well as the final velocity, so we can simply solve:
Example Question #241 : Ap Physics 1
A skydiver of mass 50kg is falling at a terminal velocity of 
Since the diver is at terminal velocity, we know that the force exerted by the air is equal to the gravitational force. Let's calculate that first:
Now that we know the force exerted by the wind, we have to connect the dots to turn this into units of power. We can do this by using the velocity of the man. Power is simply work done over time. We aren't given a time frame in the problem statement, so let's just choose a time frame of 1 second to keep things simple. Over 1 second, we know that the diver falls 75 meters. From this, we can calculate how much gravitational potential energy is lost over this distance:
This means that 37500J were exerted by the wind over a period of 1 second. Now we can simply use the formula for power:
This problem emphasizes a great tactic in solving most physics problems. If you ever get stuck, simply follow your units. See what units you have, what units you can work with, and try to figure out a logical path that combines them to get to the units that your answer should be. Although this is NOT how you should go about physics, it is a good tactic to use when you can't simply work through the problem with the concepts you have been taught.
Example Question #242 : Ap Physics 1
A man is pushing a crate through a flat warehouse at a rate of 
We first need to know the frictional force between the crate and floor:
Now that we have the frictional force, we can simply multiply it by the velocity of the crate to find power:
Example Question #243 : Ap Physics 1
A crane is being used to lift a 


First we find the total work required to lift the crate:
We are given the mass, change in height, and the acceleration of gravity. Using these values, we can solve for the total work done.
Next, we can use the equation for power to find the time to complete this task if the engine is working at its maximum power.
Example Question #2 : Power
A professional diver of mass 



We can use the equation for conservation of energy to solve for the work done by the water on the diver:
We can eliminate both kinetic energies since the diver is stationary at the initial and final states. If we assume a final height of 
That is the work done on the diver. Since we know the time period during which this work is done, we can calculate the average power of the water on the diver:
Example Question #1 : Power
Suppose that a 1000kg car accelerates from rest to 
We are given the mass of the car, its initial velocity, its final velocity, and the amount of time needed to reach its final velocity. We are then asked to calculate the power involved in the overall process. We can first start by noting that power is equal to work divided by time:
Since we are given the amount of time 

Since we're given mass, final velocity, and initial velocity, we can use these values to calculate the change in kinetic energy.
Furthermore, since the car is starting from rest, its initial velocity is equal to zero. Thus, the initial kinetic energy is equal to zero, meaning that the work done is equal to the final kinetic energy.
Substitute into the the equation for power and solve.
Example Question #8 : Power
A 5 kg box is being pulled up a ramp by a wench. This ramp has an inclination of 30 degrees and is 1 meter long. Assuming the wench pulls the box across this 1 meter in 4 seconds, what is the average power out put of the wench? Also assume the box does not change speed.
Power is most basically put as the change in energy over time.
For this problem, the only energy change we are able to consider is the change in gravititational potential energy. We are told the speed does not change so the kinetic energy is constant. The power output of the wench is going only into bringing the box higher in the gravitiational field. We ignore friction for this problem. So, rewriting the first equation:
We have the liberty to set the initial height to zero and then guage the final height starting from zero. This eliminates the initial term.
We are given the mass and time, but we need to use trig to solve for the height. We can solve for the height of the ramp using sin.

So,
Rewriting h in our power equation:
Plugging into this equation we get

Example Question #9 : Power
Determine the work needed to push a 


Assume there is no friction or air resistance.
Assume the value of the gravitational constant 
Firstly, remember that the only force in play here is gravity. Since gravity is a conservative force, to move up 





In our problem, 
Work required to move up an object is going to be:
Example Question #10 : Power
How much power does a person with a mass of 
The equation for power is given by:
Where 


However, this equation can be simplified even further:
Since we know that Force is equal to the mass times the acceleration (due to gravity in this scenario):
Here we can substitute our known values and solve for power.
Certified Tutor
All AP Physics 1 Resources