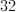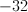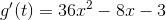All AP Calculus AB Resources
Example Questions
Example Question #1 : Derivative As A Function
A gun sends a bullet straight up with a launch velocity of 220 ft/s. It reaches a height of 


Since 

Example Question #1 : Derivative As A Function
The speed of a car traveling on the highway is given by the following function of time:
Consider a second function:
What can we conclude about this second function?
It represents another way to write the car's speed.
It has no relation to the previous function.
It represents the change in distance over a given time 
It represents the total distance the car has traveled at time 
It represents the rate at which the speed of the car is changing.
It represents the rate at which the speed of the car is changing.
Notice that the function 

Therefore, 
Example Question #204 : Ap Calculus Ab
Find the critical numbers of the function,
1) Recall the definition of a critical point:
The critical points of a function 






2) Differentiate 
3) Set to zero and solve for 
The critical numbers are,
We can also observe that the derivative does not exist at 







Further Discussion
In this problem we were asked to obtain the critical numbers. If were were asked to find the critical points, we would simply evaluate the function 
Example Question #1 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'
The function 
If the following are true:
Which function could be 
To answer this problem we must first interpret our given conditions:
-
Implies the function is strictly increasing.
-
Implies the function is strictly concave down.
We note the only function given which fufills both of these conditions is 
Example Question #4 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'
A jogger leaves City 


where 
Find the acceleration of the jogger at 
The accelaration is given by the second derivative of the position function:
For the given position function:



Therefore, the acceleration at 


Example Question #1 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'
On which interval(s) is the function 
Decreasing: 
Increasing:
Decreasing: 
Decreasing:
Increasing:
Increasing:
Decreasing:
Increasing:
Increasing:
Decreasing:
First we must find out critical points by setting 
Then we reverse foil to get

These are our critical points. We now must test values on each interval defined by our critical points in order to determine the sign of 
Our intervals to check are
We have many choices, but let's choose

Thus on our first interval 

On our second interval 

And on our third interval 

Example Question #1 : Derivative As A Function
What does the sign of the first derivative tell us about whether a function is increasing or decreasing?
If the first derivative is negative, then the function is decreasing. If the first derivative is positive, then the function is increasing.
The sign of the first derivative does not tell us anything about whether a function is increasing or decreasing.
If the first derivative is positive, then the function is decreasing. If the first derivative is negative, then the function is increasing.
If the first derivative is negative, then the function is decreasing, but if the first derivative is positive, then the function is neither increasing nor decreasing.
If the first derivative is negative, then the function is decreasing. If the first derivative is positive, then the function is increasing.
What does the sign of the first derivative tell us about whether a function is increasing or decreasing?
The first derivative test is used to tell whether a function is increasing or decreasing at a certain point or interval.
To use this test, first find the derivative of your function. Then, plug in the values for the point(s) and see what sign you get on your values.
If the value of your first derivative is negative, then your function is decreasing. If the value of your first derivative is positive, your original function is increasing. If your first derivative is 0, then you have a point of inflection in your original function.
Example Question #321 : Derivatives
Use the first derivative test to tell whether f(c) is increasing or decreasing when c=24.
Decreasing, because our first derivative is positive.
Increasing, because our first derivative is positive.
Decreasing, because our first derivative is negative.
Increasing, because our first derivative is negative.
Increasing, because our first derivative is positive.
Use the first derivative test to tell whether f(c) is increasing or decreasing when c=24
Begin by finding the first derivative of f(c)
Next, plug in 24 for c and find the sign of our first derivative.
Now, our first derivative is positive, so our original function must be increasing.
Example Question #3 : Derivative As A Function
Find the derivative of g(t) and tell whether g(t) is increasing or decreasing on the interval [5,6].
Decreasing
Decreasing
Increasing
Increasing
Decreasing
Find the derivative of g(t) and tell whether g(t) is increasing or decreasing on the interval [5,6]
First, find the derivative by decreasing each exponent by 1 and multiplying the coefficient by that number.
Next, plug in our two endpoints of our interval to see what the sign of g'(t) is.
Now, clearly these are both negative, and every point between them will be negative. This means that function g(t) is decreasing on this interval.
Example Question #5 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'
Tell whether f is increasing or decreasing when . How do you know?
f(x) is decreasing, because
f(x) is increasing, because
f(x) is decreasing, because
f(x) is increasing, because
f(x) is decreasing, because
Tell whether f is increasing or decreasing when . How do you know?
To test for increasing/decreasing, we need to find the first derivative.
In this case, we can use the power rule to do all our differentiation.
Power rule:

We will use this on each term in order to find our first and then second derivative.
For each term, we will decrease the exponent by 1, and then multiply by the original exponent.
Now, we need to find the sign of f'(-12). This will tell us if it is increasing or decreasing.
So, we get
So,
f(x) is decreasing, because
All AP Calculus AB Resources