All Algebra II Resources
Example Questions
Example Question #1 : Understanding Radicals
Simplify by rationalizing the denominator:
Multiply the numerator and the denominator by the conjugate of the denominator, which is 
Example Question #2 : Understanding Radicals
Estimate the square root of 
Recall that we are looking for a number that, when multiplied by itself, yields 









Example Question #3 : Radicals


All negative values only
All positive values only
All negative and some positive values
All positive values and some negative values
All values
All positive values only
Taking the square root of a positive number will give you a positive number, and raising any positive number to any power will result in a positive number.
Taking the square root of a negative number will result in the square root of the absolute value of the number, times i
ex. if
When an expression has 
ex. 
However, because the expression is raised to the 53rd power, it keeps the "i" in the expression for any negative value of x. Therefore, only positive numbers (and 0 which is not included in the answer choices) satisfy the requirements for being a real number.
Example Question #1 : Radicals
Estimate the square root of 110 to the nearest tenth without using a calculator`
10.4
11.1
13
10.8
9.9
10.4
The squares that are closest to 110 are 100 and 121. The square root of 100 is 10, and the square root of 121 is 11. 110 is almost right in the middle, which makes the answer 10.4.
10.9 is too high, because that would make the square closer to the 119-120 range.
Example Question #5 : Radicals
Simplify:
To simplify, we must find the squares that are underneath each radical (this can be easier to see after some factoring):
The squares are easier to identify now! We can pull them out of the radical after taking their square root, leaving behind everything that is not a square:
Example Question #6 : Radicals
Evaluate:
Simplify the radicals inside the parentheses.
Simplify the terms by order of operations. Solve the terms inside the parentheses first.
The answer is:
Example Question #1 : Understanding Radicals
Simplify the radicals:


Rewrite the numerator by taking a square root of three as a common denominator. This way, we do not have to multiply 
Notice that now we can eliminate the radical from the denominator. Fully simplify and rewrite the numerator.
Divide this by three since there is a lone three in the denominator.
The answer is:
Example Question #8 : Radicals
Evaluate the product of square roots:
We can rewrite the expression by using common factors.
The radical square root nine is a perfect square. The other two radicals can be multiplied together to form one radical.
The answer is:
Example Question #9 : Radicals
Evaluate the radical:
In order to get the most simplified answer, do not multiply all the numbers together and combine as one radical.
Rewrite each radicals in their most simplified form.
Multiply the terms.
Notice that multiplying a square root of a number by itself will leave only the integer and will eliminate the radical.
The terms become:
The answer is:
Example Question #10 : Radicals
Evaluate the square root:
The coefficients of the terms share the same square root. This means that the terms can be combined as a single square root.
Add the coefficients.
The answer is:
Certified Tutor
All Algebra II Resources
















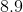











![\sqrt[3]{12}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729793/gif.latex)
![\sqrt[3]{36}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729795/gif.latex)

















































