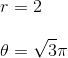Graphing Functions with Complex Numbers
Help Questions
Algebra 2 › Graphing Functions with Complex Numbers
Solve for
Explanation
Use the change of base formula for logarithmic functions and incorporate the fact that 
Or

Write the complex number 


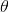
Explanation
To see what the polar form of the number is, it helps to draw it on a graph, where the horizontal axis is the imaginary part and the vertical axis the real part. This is called the complex plane.

To find the angle 



Using trigonometric ratios, 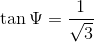

Then 
To find the distance 




Where would 
Cannot be determined
at
to the right of
to the left of
Explanation
Imaginary numbers do not fall on the number line-- they are by definition not real numbers.
** If the question asked where 

Where does 
To the right of 0
To the left of 0
At 0
Cannot be determined
Explanation
Imaginary numbers do not fall on the number line by definition, since they are not real numbers. However, although i is an imaginary number equal to the square root of -1, 


Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
Explanation
In complex numbers of the form 


Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
Explanation
In complex numbers of the form 


Which of the following represents the real component of the complex number 
Explanation
In complex numbers of the form 



Which of the following represents the imaginary component of the complex number -3 + ki, in which k is a constant?
Explanation
In complex numbers of the form 




Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
Explanation
In complex numbers of the form 


Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
Explanation
In complex numbers of the form