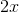All Algebra II Resources
Example Questions
Example Question #41 : Basic Single Variable Algebra
Carla wants to sell stickers to advertise her website. The machine that makes stickers costs $22, and each sticker costs $2 to make. She plans to sell these stickers for $3 each.
Write an equation that describes the number of stickers Carla would have to sell in order to break even.
Here, we can see that the independent variable is the number of stickers, so we'll call that 

So far, we have 

Now, we need to describe the revenue gained by selling 

"Breaking even" means that your costs equal your income. In other words, it's the point at which Carla's sold exactly enough stickers to make all of her initial investment back. In math, we use an equal sign to describe this. Hence, we end up with the equation:
Example Question #1 : Setting Up Expressions
Sally has 3 dollars saved. She works at the ice cream shop where she earns 5 dollars an hour. How many hours does she need to work to have enough money to buy a doll that is 23 dollars?
To set up this equation we need to put the amount of money she needs on one side of the equation and the amount of money she earns on the other side of the equation. It looks like the following
where 
From here we solve for 
Example Question #2 : Setting Up Expressions
Set up the expression to solve the following word problem:
Annie, Josh, and Brenda each have a certain number of cards. Josh has twice as many cards as Annie, and Brenda has three times as many cards as Josh. They have 
Let us call the number of cards Annie has
Josh has twice as many so we can call the number of cards Josh has
Brenda has 3 times as many cards as Josh so we can call the number of cards Brenda has
The total is 90 so we have
Which we simplify by adding all the x terms:
Example Question #43 : Basic Single Variable Algebra
A car dealer receives 



If each cars sells for 


or
or
or
The salesman will sell either more than 5 cars or less than 5.
Therefore, only one set of the equations will be true for any one month.
The word between the expressions needs to be "or."
The total profit is expressed by 30,000x.
The commision can be calculated as 
The higher commision must be matched to the equation for greater amount of cars sold, 
Example Question #263 : Equations / Inequalities
We have three cats, Chai, Sora, and Newton. Chai is 3 years old. Sora two years older than twice Chai's age. Newton is one year younger than one-fourth of Sora's age. How old are Sora and Newton?
Sora: 8 years
Newton: 1 year
Sora: 5 years
Newton: 6 years
Sora: 4 years
Newton: one half year
Sora: 1 year
Newton: 8 years
Sora: 3 years
Newton: not born yet
Sora: 8 years
Newton: 1 year
To make this much easier, translate the word problem into a system of three equations.
We have C for Chai, S for Sora, and N for Newton. To find Sora's age, plug in into
.
Sora is 8 years old. Use this to find Newton's age.
Newton is one year old. So the answer is:
Sora, 8 years
Newton, 1 year
Example Question #1 : How To Find The Missing Number In A Set
The sum of three consecutive even integers equals 72. What is the product of these integers?
12144
17472
10560
13800
13728
13728
Let us call x the smallest integer. Because the next two numbers are consecutive even integers, we can call represent them as x + 2 and x + 4. We are told the sum of x, x+2, and x+4 is equal to 72.
x + (x + 2) + (x + 4) = 72
3x + 6 = 72
3x = 66
x = 22.
This means that the integers are 22, 24, and 26. The question asks us for the product of these numbers, which is 22(24)(26) = 13728.
The answer is 13728.
Example Question #2 : Setting Up Expressions
Express as a mathematical expression.

Take every word and translate into math.


That something is 

Example Question #51 : Basic Single Variable Algebra
Express as a mathematical expression.

Take every word and translate into math.


That something is 

Example Question #3 : Expressions
Express as a mathematical expression.

Take every word and translate into math.


That something is 
Example Question #2 : Expressions
Express as a mathematical expression.
The quotient of 
Take every word and translate it into math.
Anytime you take a quotient of 



Therefore expression is
Certified Tutor
Certified Tutor
All Algebra II Resources