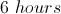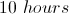Basic Single-Variable Algebra

Help Questions

Algebra 2 › Basic Single-Variable Algebra

Questions 1 - 10

Solve the equation:

$\frac{3}{2}$

$-\frac{3}{2}$

$\textup{No solution.}$

$-\frac{3}{16}$

Explanation

Use distribution to simplify the right side.

Simplify the parentheses.

Subtract on both sides.

Divide by negative 16 on both sides.

$\frac{-16x }{-16}= \frac{-24}{-16}$

Reduce both fractions.

The answer is: $\frac{3}{2}$

$\frac{2}{3}x+\frac{2}{3}=-\frac{2}{3}$

$x=-\frac{3}{2}$

$x=\frac{3}{2}$

The answer is not present

Explanation

$\frac{2}{3}x+\frac{2}{3}=-\frac{2}{3}$

Isolate the term with x:

$\frac{2}{3}x=-\frac{2}{3}-\frac{2}{3}$

Simplify:

$\frac{2}{3}x=-\frac{4}{3}$

Isolate x entirely:

$\frac{3}{2}*\frac{2}{3}x=-\frac{4}{3}*\frac{3}{2}$

$\mathbf{x=-2}$

Solve the equation:

$\frac{2}{5}$

$\frac{2}{13}$

$-\frac{2}{13}$

$\frac{20}{13}$

Explanation

Add on both sides.

Combine like-terms on both sides.

Subtract nine from both sides.

Divide by five on both sides.

$\frac{5x}{5}=\frac{2}{5}$

The answer is: $\frac{2}{5}$

$\frac{2}{3}x+\frac{2}{3}=-\frac{2}{3}$

$x=-\frac{3}{2}$

$x=\frac{3}{2}$

The answer is not present

Explanation

$\frac{2}{3}x+\frac{2}{3}=-\frac{2}{3}$

Isolate the term with x:

$\frac{2}{3}x=-\frac{2}{3}-\frac{2}{3}$

Simplify:

$\frac{2}{3}x=-\frac{4}{3}$

Isolate x entirely:

$\frac{3}{2}*\frac{2}{3}x=-\frac{4}{3}*\frac{3}{2}$

$\mathbf{x=-2}$

Tom is painting a fence feet long. He starts at the West end of the fence and paints at a rate of feet per hour. After hours, Huck joins Tom and begins painting from the East end of the fence at a rate of feet per hour. After hours of the two boys painting at the same time, Tom leaves Huck to finish the job by himself.

If Huck completes painting the entire fence after Tom leaves, how many more hours will Huck work than Tom?

$6\ hours$

$10\ hours$

$4\ hours$

$3\ hours$

$5\ hours$

Explanation

Tom paints for a total of hours (2 on his own, 2 with Huck's help). Since he paints at a rate of feet per hour, use the formula

$distance = rate \times time$ (or )

to determine the total length of the fence Tom paints.

feet

Subtracting this from the total length of the fence feet gives the length of the fence Tom will NOT paint: feet. If Huck finishes the job, he will paint that feet of the fence. Using , we can determine how long this will take Huck to do:

hours.

If Huck works hours and Tom works hours, he works more hours than Tom.

A large water tank has a water pipe that can be used to fill the tank in forty-five minutes. It has a drain that can empty the tank in one hour and twenty minutes.

One day, someone left the drain open when filling the tank. The tank was completely full by the time someone realized the error. Which of the following comes closest to the amount of time it took to fill the tank?

$1\textup{ hr }45\textup{ min}$

$1\textup{ hr }30\textup{ min}$

$2\textup{ hr }15\textup{ min}$

$2\textup{ hr }30\textup{ min}$

$2\textup{ hr }$

Explanation

Work problems can be solved by looking at them as rate problems. Therefore, we can look at this problem in terms of tanks per minute, rather than minutes per tank. Let be the number of minutes it took to fill the tank.

The pipe filled the tank at a rate of 45 minutes per tank, or $\frac{1}{45}$ tank per minute; over a period of minutes, it filled $\frac{1}{45} X$ tank.

The drain emptied the tank at a rate of 80 minutes per tank, so we can see this as a drain of $\frac{1}{80}$ tank per minute. We can look at draining as "filling negative tanks" - $-\frac{1}{80}$ tank per minute; over a period of minutes, it "filled" $-\frac{1}{80} X$ tank.

Since their work adds up to one tank filled, We can set up, and solve for in, the equation:

$\frac{1}{45} X -\frac{1}{80} X = 1$

$\left (\frac{1}{45} -\frac{1}{80} \right )X = 1$

Using decimal approximations:

$\left (0.02222 - 0.01250 \right )X = 1$

$X = 1 \div 0.00972 \approx 103$ minutes, or 1 hour 43 minutes.

Of the given choices, 1 hour 45 minutes is closest.

Solve for .

Explanation

In order to solve this equation, we need to isolate the variable, , on the left side of the equals sign. We will do this by performing the same operations on both sides of the equation.

Subtract from both sides of the equation.

Solve.

Solve for :

$3(x + 4) \leq x - 6$

$x \leq -9$

$x \leq 9$

$x \geq -9$

$x \geq 9$

$x \leq 3$

Explanation

The first step is to distribute (multiply) through the parentheses:

$3(x + 4) \leq x - 6$

$3x + 12 \leq x - 6$

Then subtract from both sides of the inequality:

$2x + 12 \leq -6$

Next, subtract the 12:

$2x \leq -18$

Finally, divide by two:

$x \leq -9$

The distance of a cyclist is directly proportional to the time he has traveled. Suppose he has traveled 12 miles in 1.5 hours. How far does he travel in a half hour?