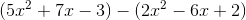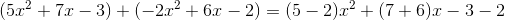All Algebra 1 Resources
Example Questions
Example Question #1 : How To Subtract Trinomials
Simpify into quadratic form:
First, FOIL the binomial combinations:
FOIL stands for the multiplication between the first terms, outer terms, inner terms, and then the last terms.
Next, distribute 
So, our answer is 
Example Question #2 : How To Subtract Trinomials
Simplify the following expression:
Let's solve this problem the long way, to see how it's done. Then we can look at a shortcut.
First, FOIL the binomial combinations:
FOIL stands for the multiplication between the first terms, outer terms, inner terms, and then the last terms.
Lastly, add the compatible terms in our trinomials:


So, our answer is 
Now, let's look at a potentially faster way.
Look at our initial problem.
Notice how 
Simpify the second term:
Now, perform a much easier multiplication:
So, our answer is 
Example Question #3 : How To Subtract Trinomials
Simplify the following:

Now we add/subtract all like terms, yielding:
Example Question #1 : How To Subtract Trinomials
Subtract 

Group both trinomials with a parenthesis and set up the expression.
Simplify by removing the parentheses, distribute the negative sign, and rewrite the expression.
Combine like-terms.
The answer is:
Example Question #4 : How To Subtract Trinomials
Simplify:
To subtract polynomials, simply combine like terms. But be extremely careful to distribute the negative to ALL terms in the second polynomial! (Consider subtracting vertically to help.)
Example Question #5 : How To Subtract Trinomials
To subtract polynomials, simply combine like terms. But be extremely careful to distribute the negative to ALL terms in the second polynomial! (Consider subtracting vertically to help.)
Example Question #6 : How To Subtract Trinomials
Simplify:
To subtract polynomials, simply combine like terms. But be extremely careful to distribute the negative to ALL terms in the second polynomial! (Consider subtracting vertically to help.)
Here, notice that the terms are not in the same order in both polynomials.
Example Question #51 : Polynomials
Find the difference.
When subtracting trinomials we distribute the negative sign and turn it into addition.
We then combine together coefficients of like terms.
Example Question #1 : Simplifying Expressions
Divide:
Factor the numerator and denominator:
Cancel the factors that appear in both the numerator and the denominator:
Example Question #1 : How To Divide Trinomials
Divide the following trinomials:
In order to divide, we must first factor both trinomials on the numerator and denominator.
Notice that we now have common terms in the numerator and denominator that can be divided and cancelled.
Cancel the 
The answer is:
All Algebra 1 Resources